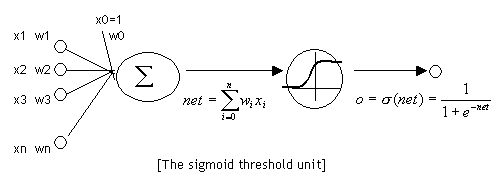
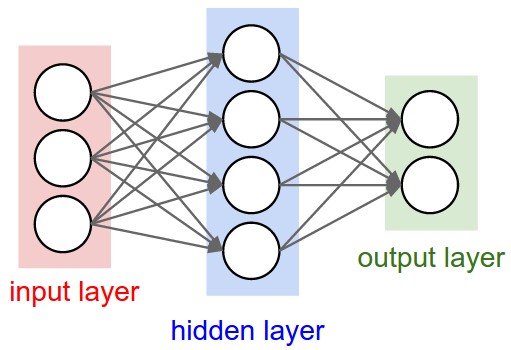
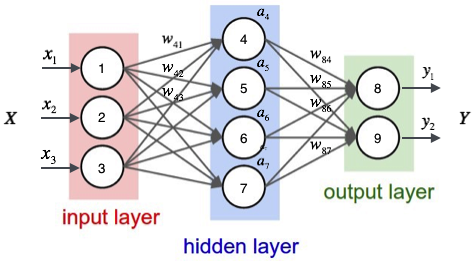
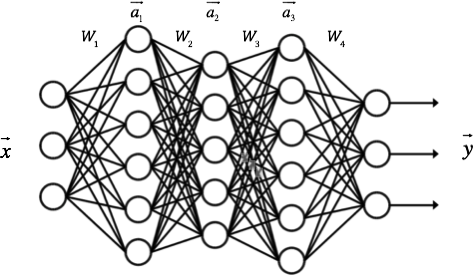
TensorFlow™ 是一个使用数据流图进行数值计算的开源软件库。图中的节点代表数学运算， 而图中的边则代表在这些节点之间传递的多维数组（张量）。这种灵活的架构可让您使用一个 API 将计算工作部署到桌面设备、服务器或者移动设备中的一个或多个 CPU 或 GPU。 TensorFlow 最初是由 Google 机器智能研究部门的 Google Brain 团队中的研究人员和工程师开发的，用于进行机器学习和深度神经网络研究， 但它是一个非常基础的系统，因此也可以应用于众多其他领域。
TensorFlow是开源数学计算引擎，由Google创造，用Apache 2.0协议发布。TF的API是Python的，但底层是C++。和Theano不同，TF兼顾了工业和研究，在RankBrain、DeepDream等项目中使用。TF可以在单个CPU或GPU，移动设备以及大规模分布式系统中使用。
神经元和感知器本质上是一样的，只不过我们说感知器的时候，它的激活函数是阶跃函数；而当我们说神经元时，激活函数往往选择为sigmoid函数或tanh函数。如下图所示：
计算一个神经元的输出的方法和计算一个感知器的输出是一样的。假设神经元的输入是向量$x$，权重向量$w$是(偏置项是$w_0$)，激活函数是sigmoid函数，则其输出$y$：
$$
y=sigmioid(w^T x )
$$
sigmoid函数的定义如下：
$$
sigmoid(x)={1\over 1+e^{-x}}
$$
将其代入前面的式子，得到
$$
y={1\over 1+e^{-w^Tx}}
$$
sigmoid函数是一个非线性函数，值域是(0,1)。函数图像如下图所示
sigmoid函数的导数是：
$$
y=sigmoid(x)…………(1)\\
y’=y(1-y)……………(2)
$$
神经网络其实就是按照一定规则连接起来的多个神经元。上图展示了一个全连接(full connected, FC)神经网络，通过观察上面的图，我们可以发现它的规则包括：
神经元按照层来布局。最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的。
同一层的神经元之间没有连接。
第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义)，第N-1层神经元的输出就是第N层神经元的输入。
每个连接都有一个权值。
上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络，比如卷积神经网络(CNN)、循环神经网络(RNN)，他们都具有不同的连接规则。
神经网络实际上就是一个输入向量$x$到输出向量$y$的函数，即：
$$
y=f_{network}(x)
$$
根据输入计算神经网络的输出，需要首先将输入向量的每个元素的值赋给神经网络的输入层的对应神经元，然后根据式1依次向前计算每一层的每个神经元的值，直到最后一层输出层的所有神经元的值计算完毕。最后，将输出层每个神经元的值串在一起就得到了输出向量。
接下来举一个例子来说明这个过程，我们先给神经网络的每个单元写上编号。
如上图，输入层有三个节点，我们将其依次编号为1、2、3；隐藏层的4个节点，编号依次为4、5、6、7；最后输出层的两个节点编号为8、9。因为我们这个神经网络是全连接网络，所以可以看到每个节点都和上一层的所有节点有连接。比如，我们可以看到隐藏层的节点4，它和输入层的三个节点1、2、3之间都有连接，其连接上的权重分别为$w_{41},w_{42},w_{43}$。那么，我们怎样计算节点4的输出值呢$a_4$？
为了计算节点4的输出值，我们必须先得到其所有上游节点（也就是节点1、2、3）的输出值。节点1、2、3是输入层的节点，所以，他们的输出值就是输入向量本身。按照上图画出的对应关系，可以看到节点1、2、3的输出值分别是$x_1,x_2,x_3$。我们要求输入向量的维度和输入层神经元个数相同，而输入向量的某个元素对应到哪个输入节点是可以自由决定的，你偏非要把$x_1$赋值给节点2也是完全没有问题的，但这样除了把自己弄晕之外，并没有什么价值。
一旦我们有了节点1、2、3的输出值，我们就可以根据式1计算节点4的输出值$a_4$
$$
a_4=sigmoid(w^Tx)………………..(3)\\
=sigmoid(w_{41}x_1+w_{42}x_2+w_{43}x_3+w_{4b})…………..(4)
$$
上式的$w_{4b}$是节点4的偏置项，图中没有画出来。而$w_{41},w_{42},w_{43}$分别为节点1、2、3到节点4连接的权重，在给权重$w_{ji}$编号时，我们把目标节点的编号$j$放在前面，把源节点的编号$i$放在后面。
同样，我们可以继续计算出节点5、6、7的输出值$a_5,a_6,a_7$。这样，隐藏层的4个节点的输出值就计算完成了，我们就可以接着计算输出层的节点8的输出值$y_1$：
$$
y_1=sigmoid(w^Ta)……………(5)\\
=sigmoid(w_{84}a_4+w_{85}a_5+w_{86}a_6+w_{87}a_7+w_{8b})……………(6)
$$
同理，我们还可以计算出的值$y_2$。这样输出层所有节点的输出值计算完毕，我们就得到了在输入向量$\vec{x}=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$时，神经网络的输出向量$\vec{y}=\begin{bmatrix}y_1\\y_2\end{bmatrix} $这里我们也看到，输出向量的维度和输出层神经元个数相同
神经网络的计算如果用矩阵来表示会很方便（当然逼格也更高），我们先来看看隐藏层的矩阵表示。
首先我们把隐藏层4个节点的计算依次排列出来：
$$
a_4=sigmoid(w_{41}x_1+w_{42}x_2+w_{43}x_3+w_{4b})\\
a_5=sigmoid(w_{51}x_1+w_{52}x_2+w_{53}x_3+w_{5b})\\
a_6=sigmoid(w_{61}x_1+w_{62}x_2+w_{63}x_3+w_{6b})\\
a_7=sigmoid(w_{71}x_1+w_{72}x_2+w_{73}x_3+w_{7b})\\
$$
接着，定义网络的输入向量$x$和隐藏层每个节点的权重向量$w$。令
$$
\begin{align}
\vec{x}&=\begin{bmatrix}x_1\\x_2\\x_3\\1\end{bmatrix}……..(7)\\
\vec{w}_4&=[w_{41},w_{42},w_{43},w_{4b}……………….(8)]\\
\vec{w}_5&=[w_{51},w_{52},w_{53},w_{5b}]…………………..(9)\\
\vec{w}_6&=[w_{61},w_{62},w_{63},w_{6b}]……………………..(10)\\
\vec{w}_7&=[w_{71},w_{72},w_{73},w_{7b}]………………(11)\\
f&=sigmoid ………………..(12)
\end{align}
$$
代入到前面的一组式子，得到
$$
\begin{align}
a_4&=f(\vec{w_4}\centerdot\vec{x})…………..(13)\\
a_5&=f(\vec{w_5}\centerdot\vec{x})…………(14)\\
a_6&=f(\vec{w_6}\centerdot\vec{x})…………(15)\\
a_7&=f(\vec{w_7}\centerdot\vec{x})…………(16)
\end{align}
$$
现在，我们把上述计算$a_4,a_5,a_6,a_7$的四个式子写到一个矩阵里面，每个式子作为矩阵的一行，就可以利用矩阵来表示它们的计算了。令
$$
\vec{a}=
\begin{bmatrix}
a_4 \\
a_5 \\
a_6 \\
a_7 \\
\end{bmatrix},\qquad W=
\begin{bmatrix}
\vec{w}_4 \\
\vec{w}_5 \\
\vec{w}_6 \\
\vec{w}_7 \\
\end{bmatrix}=
\begin{bmatrix}
w_{41},w_{42},w_{43},w_{4b} \\
w_{51},w_{52},w_{53},w_{5b} \\
w_{61},w_{62},w_{63},w_{6b} \\
w_{71},w_{72},w_{73},w_{7b} \\
\end{bmatrix}
,\qquad f(
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
.\\
.\\
.\\
\end{bmatrix})=
\begin{bmatrix}
f(x_1)\\
f(x_2)\\
f(x_3)\\
.\\
.\\
.\\
\end{bmatrix}
$$
带入前面的一组式子，得到
$$
\vec{a}=f(W\centerdot\vec{x})\qquad (式2)
$$
在式2中，$f$是激活函数，在本例中是sigmoid函数；是某一层的权重矩阵；$\vec x$是某层的输入向量；$\vec a$是某层的输出向量。式2说明神经网络的每一层的作用实际上就是先将输入向量左乘一个数组进行线性变换，得到一个新的向量，然后再对这个向量逐元素应用一个激活函数。
每一层的算法都是一样的。比如，对于包含一个输入层，一个输出层和三个隐藏层的神经网络，我们假设其权重矩阵分别为$W_1,W_2,W_3,W_4$，每个隐藏层的输出分别是$\vec a_1,\vec a_2,\vec a_3$，神经网络的输入为$\vec x$，神经网络的输入为$\vec y$，如下图所示：
则每一层的输出向量的计算可以表示为：
$$
\begin{align}
&\vec{a}_1=f(W_1\centerdot\vec{x})………(17)\\
&\vec{a}_2=f(W_2\centerdot\vec{a}_1)………(18)\\
&\vec{a}_3=f(W_3\centerdot\vec{a}_2)……..(19)\\
&\vec{y}=f(W_4\centerdot\vec{a}_3)………..(20)\\
\end{align}
$$
这就是神经网络输出值的计算方法。
现在，我们需要知道一个神经网络的每个连接上的权值是如何得到的。我们可以说神经网络是一个模型，那么这些权值就是模型的参数，也就是模型要学习的东西。然而，一个神经网络的连接方式、网络的层数、每层的节点数这些参数，则不是学习出来的，而是人为事先设置的。对于这些人为设置的参数，我们称之为超参数(Hyper-Parameters)。
接下来，我们将要介绍神经网络的训练算法：反向传播算法。
我们首先直观的介绍反向传播算法，最后再来介绍这个算法的推导。当然读者也可以完全跳过推导部分，因为即使不知道如何推导，也不影响你写出来一个神经网络的训练代码。事实上，现在神经网络成熟的开源实现多如牛毛，除了练手之外，你可能都没有机会需要去写一个神经网络。
我们假设每个训练样本为$(\vec x,\vec t)$，其中向量$\vec x$是训练样本的特征，而$\vec t$是样本的目标值。
首先，我们根据上一节介绍的算法，用样本的特征$\vec x$，计算出神经网络中每个隐藏层节点的输出$a_i$，以及输出层每个节点的输出$y_i$。
然后，我们按照下面的方法计算出每个节点的误差项$\delta_i$：
其中，$\delta_i$是节点的误差项，$y_i$是节点的输出值，$t_i$是样本对应于节点$i$的目标值。举个例子，根据上图，对于输出层节点8来说，它的输出值是$y_i$，而样本的目标值是$t_i$，带入上面的公式得到节点8的误差项$\delta_8$应该是：
$$
\delta_8=y_1(1-y_1)(t_1-y_1)
$$
$$
\delta_i=a_i(1-a_i)\sum_{k\in{outputs}}w_{ki}\delta_k\qquad(式4)
$$
其中，是$a_i$节点$i$的输出值，$w_{ki}$是节点$i$到它的下一层节点$k$的连接的权重，$\delta_k$是节点$i$的下一层节点的误差项。例如，对于隐藏层节点4来说，计算方法如下：
$$
\delta_4=a_4(1-a_4)(w_{84}\delta_8+w_{94}\delta_9)
$$
最后，更新每个连接上的权值：
$$
w_{ji}\gets w_{ji}+\eta\delta_jx_{ji}\qquad(式5)
$$
其中，$w_{ji}$是节点$i$到节点$j$的权重，$\eta$是一个成为学习速率的常数，$\delta_j$是节点$j$的误差项，$x_{ji}$是节点$i$传递给节点$j$的输入。例如，权重$w_{84}$的更新方法如下：
$$
w_{84}\gets w_{84}+\eta\delta_8 a_4
$$
类似的，权重$w_{41}$的更新方法如下
$$
w_{41}\gets w_{41}+\eta\delta_4 x_1
$$
偏置项的输入值永远为1。例如，节点4的偏置项$w_{4b}$应该按照下面的方法计算：
$$
w_{4b}\gets w_{4b}+\eta\delta_4
$$
我们已经介绍了神经网络每个节点误差项的计算和权重更新方法。显然，计算一个节点的误差项，需要先计算每个与其相连的下一层节点的误差项。这就要求误差项的计算顺序必须是从输出层开始，然后反向依次计算每个隐藏层的误差项，直到与输入层相连的那个隐藏层。这就是反向传播算法的名字的含义。当所有节点的误差项计算完毕后，我们就可以根据式5来更新所有的权重。
反向传播算法其实就是链式求导法则的应用。然而，这个如此简单且显而易见的方法，却是在Roseblatt提出感知器算法将近30年之后才被发明和普及的。对此，Bengio这样回应道：
很多看似显而易见的想法只有在事后才变得显而易见。
接下来，我们用链式求导法则来推导反向传播算法，也就是上一小节的式3、式4、式5。
前方高能预警——接下来是数学公式重灾区，读者可以酌情阅读，不必强求。
按照机器学习的通用套路，我们先确定神经网络的目标函数，然后用随机梯度下降优化算法去求目标函数最小值时的参数值。
我们取网络所有输出层节点的误差平方和作为目标函数：
$$
E_d\equiv\frac{1}{2}\sum_{i\in outputs}(t_i-y_i)^2
$$
其中，$E_d$表示是样本$d$的误差。
观察上图，我们发现权重$w_{ji}$仅能通过影响节点$j$的输入值影响网络的其它部分，设$net_j$是节点$j$的加权输入，即
$$
\begin{align}
net_j&=\vec{w_j}\centerdot\vec{x_j}………(21)\\
&=\sum_{i}{w_{ji}}x_{ji}……..(22)
\end{align}
$$
$E_d$是$net_j$的函数，而$net_j$是$w_{ji}$的函数。根据链式求导法则，可以得到：
$$
\begin{align}
\frac{\partial{E_d}}{\partial{w_{ji}}}&=\frac{\partial{E_d}}{\partial{net_j}}\frac{\partial{net_j}}{\partial{w_{ji}}}…..(23)\\
&=\frac{\partial{E_d}}{\partial{net_j}}\frac{\partial{\sum_{i}{w_{ji}}x_{ji}}}{\partial{w_{ji}}}…..(24)\\
&=\frac{\partial{E_d}}{\partial{net_j}}x_{ji}…….(24)
\end{align}
$$
上式中，$x_{ji}$是节点$i$传递给节点$j$的输入值，也就是节点$i$的输出值。
对于$\frac{\partial{E_d}}{\partial{net_j}}$的推导，需要区分输出层和隐藏层两种情况。
对于输出层来说，$net_j$仅能通过节点$j$的输出值$y_i$来影响网络其它部分，也就是说$E_d$是$y_i$的函数，而$y_i$是$net_j$的函数，其中$y_i=sigmoid(net_j)$。所以我们可以再次使用链式求导法则：
$$
\begin{align}
\frac{\partial{E_d}}{\partial{net_j}}&=\frac{\partial{E_d}}{\partial{y_j}}\frac{\partial{y_j}}{\partial{net_j}}……(26)\\
\end{align}
$$
考虑上式第一项:
$$
\begin{align}
\frac{\partial{E_d}}{\partial{y_j}}&=\frac{\partial}{\partial{y_j}}\frac{1}{2}\sum_{i\in outputs}(t_i-y_i)^2…..(27)\\
&=\frac{\partial}{\partial{y_j}}\frac{1}{2}(t_j-y_j)^2……(28)\\
&=-(t_j-y_j)
\end{align}
$$
考虑上式第二项：
$$
\begin{align}
\frac{\partial{y_j}}{\partial{net_j}}&=\frac{\partial sigmoid(net_j)}{\partial{net_j}}…..(30)\\
&=y_j(1-y_j) …….(31)\\
\end{align}
$$
将第一项和第二项带入，得到：
$$
\frac{\partial{E_d}}{\partial{net_j}}=-(t_j-y_j)y_j(1-y_j)
$$
如果令$\delta_j=-\frac{\partial{E_d}}{\partial{net_j}}$,也就是一个节点的误差项是网络误差对这个节点输入的偏导数的相反数。带入上式，得到：
$$
\delta_j=(t_j-y_j)y_j(1-y_j)
$$
上式就是式3。
将上述推导带入随机梯度下降公式，得到：
$$
\begin{align}
w_{ji}&\gets w_{ji}-\eta\frac{\partial{E_d}}{\partial{w_{ji}}}…….(32)\\
&=w_{ji}+\eta(t_j-y_j)y_j(1-y_j)x_{ji}………(33)\\
&=w_{ji}+\eta\delta_jx_{ji}……..(34)
\end{align}
$$
上式就是式5。
现在我们要推导出隐藏层的$\frac{\partial{E_d}}{\partial{net_j}}$。
首先，我们需要定义节点$j$的所有直接下游节点的集合$Downstream(j)$。例如，对于节点4来说，它的直接下游节点是节点8、节点9。可以看到只能通过影响$Downstream(j)$再影响$E_d$。设$net_k$是节点$j$的下游节点的输入，则$E_d$是$net_k$的函数，而$net_k$是$net_j$的函数。因为$net_k$有多个，我们应用全导数公式，可以做出如下推导：
$$
\begin{align}
\frac{\partial{E_d}}{\partial{net_j}}&=\sum_{k\in Downstream(j)}\frac{\partial{E_d}}{\partial{net_k}}\frac{\partial{net_k}}{\partial{net_j}}…..(35)\\
&=\sum_{k\in Downstream(j)}-\delta_k\frac{\partial{net_k}}{\partial{net_j}}……….(36)\\
&=\sum_{k\in Downstream(j)}-\delta_k\frac{\partial{net_k}}{\partial{a_j}}\frac{\partial{a_j}}{\partial{net_j}}……(37)\\
&=\sum_{k\in Downstream(j)}-\delta_kw_{kj}\frac{\partial{a_j}}{\partial{net_j}}……..(38)\\
&=\sum_{k\in Downstream(j)}-\delta_kw_{kj}a_j(1-a_j)………(39)\\
&=-a_j(1-a_j)\sum_{k\in Downstream(j)}\delta_kw_{kj}…….(40)
\end{align}
$$
因为$\delta_j=-\frac{\partial{E_d}}{\partial{net_j}}$，带入上式得到：
$$
\delta_j=a_j(1-a_j)\sum_{k\in Downstream(j)}\delta_kw_{kj}
$$
上式就是式4。
——数学公式警报解除——
至此，我们已经推导出了反向传播算法。需要注意的是，我们刚刚推导出的训练规则是根据激活函数是sigmoid函数、平方和误差、全连接网络、随机梯度下降优化算法。如果激活函数不同、误差计算方式不同、网络连接结构不同、优化算法不同，则具体的训练规则也会不一样。但是无论怎样，训练规则的推导方式都是一样的，应用链式求导法则进行推导即可。
1 | for l in range(len(self.weights)): |
感知器有一个问题，当面对的数据集不是线性可分的时候，『感知器规则』可能无法收敛，这意味着我们永远也无法完成一个感知器的训练。为了解决这个问题，我们使用一个可导的线性函数来替代感知器的阶跃函数，这种感知器就叫做线性单元。线性单元在面对线性不可分的数据集时，会收敛到一个最佳的近似上。
为了简单起见，我们可以设置线性单元的激活函数$f$为
$f(x)=x$
这样的线性单元如下图所示
感知器
替换激活函数之后，线性单元将返回一个实数值而不是0,1分类。因此线性单元用来解决回归问题而不是分类问题。
当我们说模型时，我们实际上在谈论根据输入$x$预测输出$y$的算法。比如，$x$可以是一个人的工作年限，$y$可以是他的月薪，我们可以用某种算法来根据一个人的工作年限来预测他的收入。比如：
$y=h(x)=w*x+b$
函数$h(x)$叫做假设，而$w,b$是它的参数。我们假设参数$w=1000$，参数$b=500$，如果一个人的工作年限是5年的话，我们的模型会预测他的月薪为
$y=h(x)=1000*5+500=5500（元）$
你也许会说，这个模型太不靠谱了。是这样的，因为我们考虑的因素太少了，仅仅包含了工作年限。如果考虑更多的因素，比如所处的行业、公司、职级等等，可能预测就会靠谱的多。我们把工作年限、行业、公司、职级这些信息，称之为特征。对于一个工作了5年，在IT行业，百度工作，职级T6这样的人，我们可以用这样的一个特征向量来表示他
$x=(5,IT,百度，T6)$
既然输入$x$变成了一个具备四个特征的向量，相对应的，仅仅一个参数$w$就不够用了，我们应该使用4个参数$w_1,w_2,w_3,w_4$，每个特征对应一个。这样，我们的模型就变成
$y=h(x)=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b$
其中，$x_1$对应工作年限，$x_2$对应行业，$x_3$对应公司，$x_4$对应职称。
为了书写和计算方便，我们可以$w_0$令等于$b$，同时令$w_0$对应于特征$x_0$。由于$x_0$其实并不存在，我们可以令它的值永远为1。也就是说
$b=w_0*x_0$ 其中$x_0=1$
这样上面的式子就可以写成
$y=h(x)=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b$ ………….(1)
$=w_0x_0+w_1x_1+w_2x_2+w_3x_3+w_4*x_4$ ………….(2)
我们还可以把上式写成向量的形式
$y=h(x)=w^Tx$
长成这种样子模型就叫做线性模型，因为输出$y$就是输入特征$x_1,x_2,x_3,…$的线性组合。
接下来，我们需要关心的是这个模型如何训练，也就是参数$w$取什么值最合适。
机器学习有一类学习方法叫做监督学习，它是说为了训练一个模型，我们要提供这样一堆训练样本：每个训练样本既包括输入特征$x$，也包括对应的输出$y$(也叫做标记，label)。也就是说，我们要找到很多人，我们既知道他们的特征(工作年限，行业…)，也知道他们的收入。我们用这样的样本去训练模型，让模型既看到我们提出的每个问题(输入特征)，也看到对应问题的答案(标记)。当模型看到足够多的样本之后，它就能总结出其中的一些规律。然后，就可以预测那些它没看过的输入所对应的答案了。
另外一类学习方法叫做无监督学习，这种方法的训练样本中只有而没有。模型可以总结出特征的一些规律，但是无法知道其对应的答案$y$。
很多时候，既有$x$又有的$y$训练样本是很少的，大部分样本都只有$x$。比如在语音到文本(STT)的识别任务中，$x$是语音，$y$是这段语音对应的文本。我们很容易获取大量的语音录音，然而把语音一段一段切分好并标注上对应文字则是非常费力气的事情。这种情况下，为了弥补带标注样本的不足，我们可以用无监督学习方法先做一些聚类，让模型总结出哪些音节是相似的，然后再用少量的带标注的训练样本，告诉模型其中一些音节对应的文字。这样模型就可以把相似的音节都对应到相应文字上，完成模型的训练。
现在，让我们只考虑监督学习。
在监督学习下，对于一个样本，我们知道它的特征$x$，以及标记$y$。同时，我们还可以根据模型计算得到输出。注意这里面我们用表示训练样本里面的标记，也就是实际值；用带上划线的表示模型计算的出来的预测值。我们当然希望模型计算出来的和越接近越好。
数学上有很多方法来表示的$\overline y$和$y$的接近程度，比如我们可以用$\overline y$和$y$的差的平方的$1\over2$来表示它们的接近程度
$e={1\over2}(y-\overline y)^2$
我们把$e$叫做单个样本的误差。至于为什么前面要乘$1\over 2$，是为了后面计算方便。
训练数据中会有很多样本，比如$N$个，我们可以用训练数据中所有样本的误差的和，来表示模型的误差$E$，也就是$E=e^{(1)}+e^{(2)}+e^{(3)}+\dots+e^{(n)}$
上式的$e^{(1)}$表示第一个样本的误差，$e^{(2)}$表示第二个样本的误差……。
我们还可以把上面的式子写成和式的形式。使用和式，不光书写起来简单，逼格也跟着暴涨，一举两得。所以一定要写成下面这样
$E=e^{(1)}+e^{(2)}+e^{(3)}+\dots+e^{(n)}$ …………………(3)
$\sum_{i=1}^n e^{(i)} $ …………………(4)
$={1\over 2}\sum_{i=1}^n(y^(i)-\overline y^{(i)})^2$ . …………………(5)
其中
$\overline y^{(i)}=h(x^{(i)})$ ……………………..(6)
$=w^Tx^{(i)}$ ………………………..(7)
(5)中，$x^{(i)}$表示第$i$个训练样本的特征，$y^{(i)}$表示第$i$个样本的标记，我们也可以用元组$(x^{(i)},y^{(i)})$表示第$i$个 训练样本。$\overline y^{(i)}$则是模型对第$i$个样本的预测值。
我们当然希望对于一个训练数据集来说，误差最小越好，也就是(5)的值越小越好。对于特定的训练数据集来说，$(x^{(i)},y^{(i)})$的值都是已知的，所以(式2)其实是参数$w$的函数。
$E(w)={1\over 2}\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})^2 $ ……………………..(8)
$={1\over 2}\sum_{i=1}^n(y^{(i)}-w^Tx^{(i)})^2$ ………………………….(9)
由此可见，模型的训练，实际上就是求取到合适的，使(5)取得最小值。这在数学上称作优化问题，而就是我们优化的目标，称之为目标函数。
我们学过怎样求函数的极值。函数$y=f(x)$的极值点，就是它的导数$f’(x)=0$的那个点。因此我们可以通过解方程$f’(x)=0$，求得函数的极值点$(x_0,y_0)$。
不过对于计算机来说，它可不会解方程。但是它可以凭借强大的计算能力，一步一步的去把函数的极值点『试』出来。如下图所示：
首先，我们随便选择一个点开始，比如上图的点$x_0$。接下来，每次迭代修改$x$的为，经过数次迭代后最终达到函数最小值点。
你可能要问了，为啥每次修改的值，都能往函数最小值那个方向前进呢？这里的奥秘在于，我们每次都是向函数$y=f(x)$的梯度的相反方向来修改$x$。什么是梯度呢？梯度是一个向量，它指向函数值上升最快的方向。显然，梯度的反方向当然就是函数值下降最快的方向了。我们每次沿着梯度相反方向去修改的值，当然就能走到函数的最小值附近。之所以是最小值附近而不是最小值那个点，是因为我们每次移动的步长不会那么恰到好处，有可能最后一次迭代走远了越过了最小值那个点。步长的选择是门手艺，如果选择小了，那么就会迭代很多轮才能走到最小值附近；如果选择大了，那可能就会越过最小值很远，收敛不到一个好的点上。
按照上面的讨论，我们就可以写出梯度下降算法的公式
$x_{new}=x_{old}-\eta\nabla f(x)$
其中，$\nabla$是梯度算子，$\nabla f(x)$就是指的梯度。$\eta$是步长，也称作学习速率。
对于上一节列出的目标函数(式5)
$E(w)={1\over2}\sum_{i=1}^n(y^{(i)}-\overline y^{(i)}$
梯度下降算法可以写成
$w_{new}=w_{old}+\eta\nabla E(w)$
我们要来求取$\nabla E(w)$，然后带入上式，就能得到线性单元的参数修改规则。
关于$\nabla E(w)$的推导过程，我单独把它们放到一节中。您既可以选择慢慢看，也可以选择无视。在这里，您只需要知道，经过一大串推导，目标函数$E(w)$的梯度是
$\nabla E(w)=-\sum_{i=1}^{n}(y^{(i)}-\overline y^{(i)})x^{(i)}$
因此，线性单元的参数修改规则最后是这个样子
$w_{new}=w_{old}+\eta\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})$
有了上面这个式子，我们就可以根据它来写出训练线性单元的代码了。
需要说明的是，如果每个样本有M个特征，则上式w，x都是M+1维向量（因为我们加上了一个恒为1的虚拟特征$x_0$,参考前面的内容），而$y$是标量。用高逼格的数学符号表示 ，就是
$w,x\in R^{(M+1)}$
$y\in R^1$
为了让您看明白说的是啥，我吐血写下下面这个解释(写这种公式可累可累了)。因为$w,x$是M+1维列向量，所以(式3)可以写成
$$
\begin{bmatrix}
w_0 \\
w_1\\
w_2\\
\dots\\
w_m\\
\end{bmatrix}=\begin{bmatrix}
w_0 \\
w_1\\
w_2\\
\dots\\
w_m\\
\end{bmatrix}+\eta\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})\begin{bmatrix}
1 \\
x_1^{(i)}\\
x_2^{(i)}\\
\dots\\
x_m^{(i)}\\
\end{bmatrix}
$$
这一节你尽可以跳过它，并不太会影响到全文的理解。当然如果你非要弄明白每个细节，那恭喜你骚年，机器学习的未来一定是属于你的。
首先，我们先做一个简单的前戏。我们知道函数的梯度的定义就是它相对于各个变量的偏导数，所以我们写下下面的式子
$$
\nabla E(w)={\partial\over\partial w}E(w) …………….(10)\\
={\partial\over \partial w}{1\over2}\sum_{i=1}^n(y^{(i)} - \overline y^{(i)})………….(11)
$$
可接下来怎么办呢？我们知道和的导数等于导数的和，所以我们可以先把求和符号$\sum$里面的导数求出来，然后再把它们加在一起就行了，也就是
$$
{\partial \over \partial w }{1\over 2}\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})^2…………(12)\\
={1\over 2}\sum_{i=1}^n{\partial\over \partial w}(y^{(i)}-\overline y^{(i)})^2…………(13)
$$
现在我们可以不管高大上的$\sum$了，先专心把里面的导数求出来。
$$
{\partial \over \partial w}(y^{(i)}-\overline y^{(i)})^2………………….(14)\\
={\partial \over \partial w}({y^{(i)}}^2-2\overline y^{(i)} +{\overline y^{(i)}}^2)………………….(15)
$$
我们知道，$y$是与$w$无关的常数，而$\overline y=w^Tx$,下面我们根据链式求导法则来求导。
$$
{\partial E(w)\over \partial w}={\partial E(\overline y)\over \partial\overline y}{\partial\overline y\over \partial w}
$$
我们分别计算上式等号右边的两个偏导数
$$
{\partial E(w)\over \partial \overline y}={\partial \over\partial \overline y}({y^{(i)}}^2-2\overline y^{(i)}y^{(i)}+{\overline y^{(i)}}^2)…………(16)\\
=-2y^{(i)}+2\overline y ^{(i)}……………….(17)
$$
$$
{\partial \overline y \over \partial w}={\partial \over\partial w}w^Tx ……………………..(18)\\
=x……………………(19)
$$
代入，我们求得$\sum$里面的偏导数是
$$
{\partial \over \partial w}(y^{(i)}-\overline y^{(i)})^2………………………..(20)\\
=2(-y^{(i)}+\overline y^{(i)})x……………………….(21)
$$
最后代入$\nabla E(w)$,求得
$$
\nabla E(w)={1\over2}\sum_{i=1}^n{\partial\over \partial w}(y^{(i)}-\overline y^{(i)})^2…………..(22)\\
={1\over 2}\sum_{i=1}^n2(-y^{(i)}+\overline y^{(i)})x…………….(23)\\
=-\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})x……………….(25)
$$
如果我们根据上面式子来训练模型，那么我们每次更新的迭代，要遍历训练数据中所有的样本进行计算，我们称这种算法叫做批梯度下降(Batch Gradient Descent)。如果我们的样本非常大，比如数百万到数亿，那么计算量异常巨大。因此，实用的算法是SGD算法。在SGD算法中，每次更新的迭代，只计算一个样本。这样对于一个具有数百万样本的训练数据，完成一次遍历就会对更新数百万次，效率大大提升。由于样本的噪音和随机性，每次更新并不一定按照减少的方向。然而，虽然存在一定随机性，大量的更新总体上沿着减少的方向前进的，因此最后也能收敛到最小值附近。下图展示了SGD和BGD的区别
如上图，椭圆表示的是函数值的等高线，椭圆中心是函数的最小值点。红色是BGD的逼近曲线，而紫色是SGD的逼近曲线。我们可以看到BGD是一直向着最低点前进的，而SGD明显躁动了许多，但总体上仍然是向最低点逼近的。
最后需要说明的是，SGD不仅仅效率高，而且随机性有时候反而是好事。今天的目标函数是一个『凸函数』，沿着梯度反方向就能找到全局唯一的最小值。然而对于非凸函数来说，存在许多局部最小值。随机性有助于我们逃离某些很糟糕的局部最小值，从而获得一个更好的模型。
事实上，一个机器学习算法其实只有两部分
模型 从输入特征预测输入的那个函数
目标函数 目标函数取最小(最大)值时所对应的参数值，就是模型的参数的最优值。很多时候我们只能获得目标函数的局部最小(最大)值，因此也只能得到模型参数的局部最优值。
因此，如果你想最简洁的介绍一个算法，列出这两个函数就行了。
接下来，你会用优化算法去求取目标函数的最小(最大)值。[随机]梯度{下降|上升}算法就是一个优化算法。针对同一个目标函数，不同的优化算法会推导出不同的训练规则。我们后面还会讲其它的优化算法。
其实在机器学习中，算法往往并不是关键，真正的关键之处在于选取特征。选取特征需要我们人类对问题的深刻理解，经验、以及思考。而神经网络算法的一个优势，就在于它能够自动学习到应该提取什么特征，从而使算法不再那么依赖人类，而这也是神经网络之所以吸引人的一个方面。
现在，经过漫长的烧脑，你已经具备了学习神经网络的必备知识。下一篇文章，我们将介绍本系列文章的主角：神经网络，以及用来训练神经网络的大名鼎鼎的算法：反向传播算法。至于现在，我们应该暂时忘记一切，尽情奖励自己一下吧。
首先介绍逻辑斯谛分布，该分布的定义是
设$X$是连续随机变量,$X$服从逻辑斯谛分布是指$X$ 服从如下分布函数和密度函数:
$F(x)=P(X\le x)={1\over 1+e^{-(x-\mu)}/\gamma}$ …………..(1)
$f(x)=F^,(X\le x)={e^{-(x-\mu)/\gamma}\over \gamma(1+e^{-(x-\mu)/\gamma})}$ …………(2)
式中，$\mu$为位置参数 ，$\gamma>0$ 为形状参数。
极大似然估计法（$Method of Maximum Likelihood Estimation –MLE$）
极大似然估计法最早由高斯（C.F.Gauss）提出。后来为费歇在1912年的文章中重新提出，并且证明了这个方法的一些性质。极大似然估计这一名称也是费歇（R.A.Fisher）给的。这是一种目前仍然得到广泛应用的方法。它是建立在极大似然原理的基础上的一个统计方法。
在数理统计学中，似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。 似然函数在统计推断中有重大作用，如在最大似然估计和费雪信息之中的应用等等。“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性，但是在统计学中，“似然性”和“或然性”或“概率”又有明确的区分。概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。 有人说，概率是已知模型和参数，推数据。统计是已知数据，推模型和参数。
极大似然估计法的依据就是：概率最大的事件最可能发生
1 | import matplotlib.pyplot as plt |
第1句，这是导入Matplotlib接口的主要子模块pyplot绘图的首选格式。这是最好的做法，也是为了避免对全局名称空间的污染，强烈鼓励永远不要像这样导入接口：
1 | from <module> import * |
第2句，此代码行是实际的绘图命令。我们只指定了一个值列表，这些值表示要绘制的点的垂直坐标。matplotlib将使用一个隐式的水平值列表，从0（前值）到n-1（n为列表中的条目数），纵轴表示Y轴，横坐标表示X轴。
第3句，这条命令实际上是打开包含绘图图像的窗口。
1 | uname -a |
1) lscpu:显示CPU架构信息
$ lscpu
1 | Architecture: x86_64 |
显示linux任务。top程序提供运行系统的动态实时视图。它可以显示系统概要信息以及当前由Linux内核管理的任务列表。所显示的系统摘要信息的类型以及任务所显示的信息的类型、顺序和大小都是用户可配置的，并且可以在重新启动时对该配置进行持久化。
1 | top(选项) |
1 | -b：以批处理模式操作； |
今天又遇到换行符的错误。想起以前换行符中遇到的坑。在不同的操作系统默认的换行符不一样，字符处理的时候会遇到一些莫名奇妙的问题。windows的换行是\r\n，linux的是\n，mac的是\r。在网络编程中，如果把Windows的一个文件数据传输到linux系统中的另一个文件，如果计算两个文件的字节数会发现两个系统同样的文本数据字节数会不一样。就是因为换行符导致的，通常模式下，换行符，空格等都是空白符，不可见的。在notepad++中视图显示所有字符会发现Windows中的换行符为CRLF，而linux中换行符为LF。利用notepad++可以将Windows文本文件转换为unix格式的文件。
special symbol in markdown
http://www.math.harvard.edu/texman/node21.html#SECTION00084000000000000000
| 两个quad空格 | a \qquad b | ab | 两个m的宽度 |
|---|---|---|---|
| quad空格 | a \quad b | ab | 一个m的宽度 |
| 大空格 | a b | a b | 1/3m宽度 |
| 中等空格 | a\;b | ab | 2/7m宽度 |
| 小空格 | a\,b | ab | 1/6m宽度 |
| 没有空格 | ab | ab | 正常宽度 |
| 紧贴 | a!b | ab | 缩进1/6m宽度 |
偏导 \partial $ \partial$