1、MNIST数据集介绍
首先介绍MNIST数据集。如果所示,MNIST数据集主要由一些手写数字的图片和相应的标签组成,图片一共有10类,分别对应0~9,共10个阿拉伯数字。如下图:
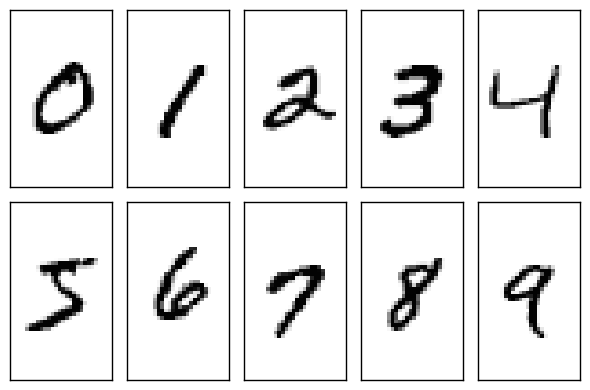
MNIST 数据集可在 http://yann.lecun.com/exdb/mnist/ 获取, 它包含了四个部分:
- Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
- Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
- Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)
- Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)
MNIST 数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员. 测试集(test set) 也是同样比例的手写数字数据。 60,000 个训练样本和 10,000 个测试样本.


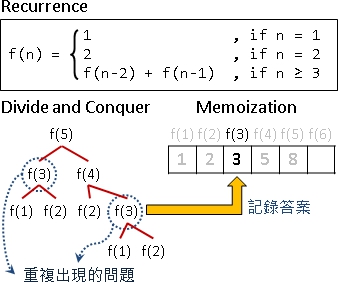
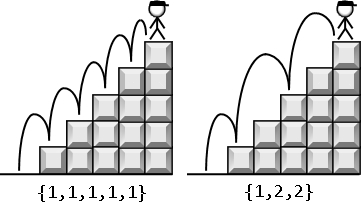

 带入实际数值,递归计算即可。
带入实际数值,递归计算即可。