tensorflow入门笔记1

发表于 | 分类于 |

1、MNIST数据集介绍

        首先介绍MNIST数据集。如果所示，MNIST数据集主要由一些手写数字的图片和相应的标签组成，图片一共有10类，分别对应0~9，共10个阿拉伯数字。如下图：

1

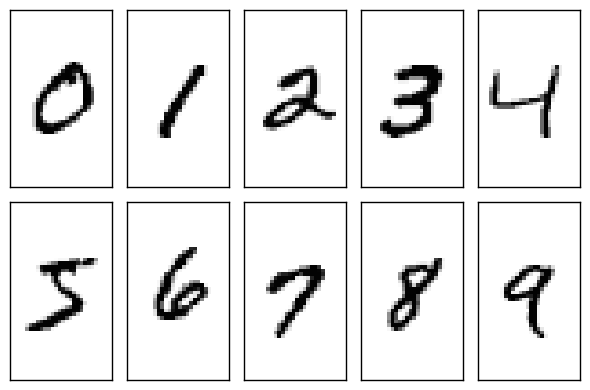
MNIST 数据集可在 http://yann.lecun.com/exdb/mnist/ 获取, 它包含了四个部分:

  • Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
  • Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
  • Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)
  • Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)

        MNIST 数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员. 测试集(test set) 也是同样比例的手写数字数据。 60,000 个训练样本和 10,000 个测试样本.

2、下载数据集

1
2
3
4
# 从tensorflow.examples.tutorials.mnist引入模块。这是TensorFlow为了教学MNIST而提前编制的程序
from tensorflow.examples.tutorials.mnist import input_data
# 从MNIST_data/中读取MNIST数据。这条语句在数据不存在时，会自动执行下载
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

        在执行语句mnist = input_data.read_data_sets(“MNIST_data/“, one_hot=True)时，Tensorflow会检测数据是否存在。当数据不存在时，系统自动将数据下载到MNIST_data/文件夹中。当执行完语句后，可以看到MNIST_data/文件夹下多了4个上述文件。

        成功加载数据后，得到了一个mnist对象，可以通过mnist对象的数学访问到MNIST数据集。

属性名 内容 大小
mnist.train,images 训练图像 (55000,784)
mnist.train.label 训练标签 (55000,10)
mnist.validation.images 验证图像 （5000,784）
mnist.validation.labels 验证标签 （5000,10）
mnist.test.images 测试图像 （10000,784）
mnist.test.labels 测试标签 （10000,10）

        运行下面代码可以查看各个变量的形状大小：

1
2
3
4
5
6
7
8
9
10
11
# 查看训练数据的大小
print(mnist.train.images.shape)  # (55000, 784)
print(mnist.train.labels.shape)  # (55000, 10)

# 查看验证数据的大小
print(mnist.validation.images.shape)  # (5000, 784)
print(mnist.validation.labels.shape)  # (5000, 10)

# 查看测试数据的大小
print(mnist.test.images.shape)  # (10000, 784)
print(mnist.test.labels.shape)  # (10000, 10)

         原始的MNIST数据集中包含了60000张训练图片和10000张测试图片。而在tensorflow中，又将原先的60000张训练图片重新划分成了新的55000张训练图片和5000张验证图片。所以在mnist对象中，数据一共分为三部分：mnist.train是训练图片数据，mnist.validation是验证图片数据，mnist.test是测试图片数据，这正好对应了机器学习中额训练集、验证集和测试集、一般来说，会在训练集上训练模型，通过在验证集上调整参数，最后通过测试集确定模型的性能。

MNIST数据集保存为图片

为了加深理解，将MNIST数据集读取出来，并保存为图片文件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from tensorflow.examples.tutorials.mnist import input_data
import scipy.misc
import os

# 读取MNIST数据集。如果不存在会事先下载。
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 我们把原始图片保存在MNIST_data/raw/文件夹下
# 如果没有这个文件夹会自动创建
save_dir = 'MNIST_data/raw/'
if os.path.exists(save_dir) is False:
    os.makedirs(save_dir)

# 保存前20张图片
for i in range(20):
    # 请注意，mnist.train.images[i, :]就表示第i张图片（序号从0开始）
    image_array = mnist.train.images[i, :]
    # TensorFlow中的MNIST图片是一个784维的向量，我们重新把它还原为28x28维的图像。
    image_array = image_array.reshape(28, 28)
    # 保存文件的格式为 mnist_train_0.jpg, mnist_train_1.jpg, ... ,mnist_train_19.jpg
    filename = save_dir + 'mnist_train_%d.jpg' % i
    # 将image_array保存为图片
    # 先用scipy.misc.toimage转换为图像，再调用save直接保存。
    scipy.misc.toimage(image_array, cmin=0.0, cmax=1.0).save(filename)

print('Please check: %s ' % save_dir)

3、图像标签的独热表示

        变量mnist.train.labels表示训练数据的标签，它的形状是(55000,10)。原始的图像标签是数字0-9，我们完全可以用一个数字来存储图像标签，但为什么这里每个训练标签是一个10维的向量呢？其实，这个10维的向量是原先类别的独热(one-hot)表示。

4、Softmax回归识别MNIST

        softmax回归是一个线性的多分类模型，实际上它是从Logistic回归模型转化而来的。区别是Logistic回归模型是一个两分类模型，而Softmax模型为多分类模型。

        在手写体识别问题中，一共有10个类别(0~9)，我们希望对输入的图像计算它属于每个类别的概率。如属于9的概率为70%，属于1的概率为10%等。最后模型预测的结果就是概率最大的那个类别。

        先来了解什么是Softmax函数。Softmax函数的主要功能是将各个类别的“打分“转化成合理的概率值。例如，一个样本可能属于三个类别：第一个类别的打分为a，第二个类别的打分为b，第三个类别的打分为c。打分越高代表属于这个类别的概率越高，但是打分本身不代表概率，因为打分的值可以使负数，也可以很大。但概率要求值必须在0~1，并且三类的概率加起来等于1.那么，如何将(a,b,c)转换成合理的概率值呢？方法就是使用Softmax函数。例如，对(a,b,c)使用softmax函数后，相异的值会变成$({e^a \over e^a+e^b+e^c},{e^b \over e^a+e^b+e^c},{e^c \over e^a+e^b+e^c})$，也就是说，第一类的概率用$e^a \over e^a+e^b+e^c$来表示，第二类用$e^b \over e^a+e^b+e^c$来表示，第三类可以用$e^c \over e^a+e^b+e^c$来表示。显然，这三个数都在0~1之间，并且加起来正好等于1，是合理的概率表示。

        假设$x$是单个样本的特征，$W,b$是Softmax模型的参数。在MNIST数据集中，$x$就代表输入图片，它是一个784维的向量，而$W$是一个矩阵，它的形状为(784,10),$b$是一个10维的向量，10代表的是类别数。Softmax模型的第一步是通过下面的公司计算各个类别的Logit：
$$
Logit=W^Tx+b
$$
        Logit同样是一个10维的向量，它的实际上可以看出样本对于于各个类别的“打分”。接下来使用Softmax函数将他转换成各个类别的概率值：
$$
y=Softmax(Logit)
$$
        Softmax模型输出的y代表各个类别的概率，还可以直接用下面的式子来表示整个Softmax模型：
$$
y=Softmax(W^Tx+b)
$$

##5、Softmax实现

        首先导入tensorflow模型,下面是约定俗成的写法：

1
import tensorflow as tf

        接下来导入MNIST数据集

1
2
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

        构建模型

1
2
3
4
5
6
7
8
9
10
11
12
# 创建x，x是一个占位符（placeholder），代表待识别的图片
x = tf.placeholder(tf.float32, [None, 784])
# W是Softmax模型的参数，将一个784维的输入转换为一个10维的输出
# 在TensorFlow中，变量的参数用tf.Variable表示
W = tf.Variable(tf.zeros([784, 10]))
# b是又一个Softmax模型的参数，我们一般叫做“偏置项”（bias）。
b = tf.Variable(tf.zeros([10]))

# y=softmax(Wx + b)，y表示模型的输出
y = tf.nn.softmax(tf.matmul(x, W) + b)
# y_是实际的图像标签，同样以占位符表示。
y_ = tf.placeholder(tf.float32, [None, 10])

        这里定义了一下占位符(placeholder)和变量(Variable).在tensorflow中无论是占位符还是变量，它们实际上都是“Tensor”。从Tensorflow的名字中就可以看出Tensor在整个系统处于核心地位。Tensor并不是具体的数值，它只是一些我们”希望“Tensorflow系统计算的“节点”。

        这里的占位符和变量是不同类型的Tensor。先来讲解占位符。占位符不依赖于其它的Tensor，它的值由用户自行传到给Tensorflow，通常用来存储样本数据和标签。如在这里定义了x = tf.placeholder(tf.float32, [None, 784])，它是用来存储训练图片数据的占位符，它的形状为[None, 784]，None表示这一维的大小是任意的，也就是说可以传递任意章训练图片给这个占位符，每张图片用784维的向量表示。同样的，y_ = tf.placeholder(tf.float32, [None, 10])也是一个占位符，它存储训练图片的实际标签。

        再来看什么是变量，变量是指在计算过程中可以改变的值，每次计算后变量的值会被保存下来，通常用变量来存储模型的参数。如：W = tf.Variable(tf.zeros([784, 10]))。创建变量时通常要指定某些初始值。

        除了变量和占位符之外，还创建了一个y

1
y = tf.nn.softmax(tf.matmul(x, W) + b)

        这个y就是一个依赖x，W，b的Tensor。如果要求Tensorflow计算y的值，那么系统首先会获取$x,W,b$的值，再去计算y的值

        y实际上定义了一个Softmax回归模型，在此可以尝试写出y的形状。假设输入x的形状为(N,784)，其中N表示输入的训练图像的数目。W的形状为（784,10），b的形状为（10），那么Wx+b的形状是(N,10)。Softmax函数不改变结果的形状，所以得到y的形状为(N,10)。也就是说，y的每一行是10维的向量，表示模型预测的样本对应到各个类别的概率。

        模型的输出是y，而实际的标签为y_,它们应当越相似越好。在Softmax回归模型中，通常使用“交叉熵”损失来衡量相似性。损失越小，模型的输出就和实际标签越接近，模型的预测也就越准确。

        在Tensorflow中，这样定义交叉熵损失：

1
2
# 根据y, y_构造交叉熵损失
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y)))

        构造玩损失之后，下面一步是如何优化损失，让损失减小。这里使用梯度下降优化损失，定义为

1
2
# 有了损失，我们就可以用随机梯度下降针对模型的参数（W和b）进行优化
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

​ Tensorfloe默认会对所有变量计算梯度。这里只定义两个变量$W$和$b$，因此程序将会使用梯度下降法对$W,b$计算梯度并更新它们的值。

        在优化之前，必须要创建一个会话(Session),并在会话中对变量进行初始化操作：

1
2
3
4
# 创建一个Session。只有在Session中才能运行优化步骤train_step。
sess = tf.InteractiveSession()
# 运行之前必须要初始化所有变量，分配内存。
tf.global_variables_initializer().run()

        有了会话，就可以对变量进行优化了，优化的程序如下：

1
2
3
4
5
6
7
for _ in range(1000):
    # 在mnist.train中取100个训练数据
    # batch_xs是形状为(100, 784)的图像数据，batch_ys是形如(100, 10)的实际标签
    # batch_xs, batch_ys对应着两个占位符x和y_
    batch_xs, batch_ys = mnist.train.next_batch(100)
    # 在Session中运行train_step，运行时要传入占位符的值
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

        与变量不同的是，占位符的值不会被保存，每次可以给占位符传递不同的值。

​ 训练完成后，可以检测模型训练的结果，对于的代码如下：

1
2
3
4
5
6
7
# 正确的预测结果
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
# 计算预测准确率，它们都是Tensor
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 在Session中运行Tensor可以得到Tensor的值
# 这里是获取最终模型的正确率
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))  # 0.9052

        模型预测y的形状是(N,10)，而实际标签y_的形状是(N,10)，其中N为输入模型1的样本数。tf.argmax(y,1)、tf.argmax(y_,1)的功能是取出数组最大值得下标，可以用来将独热表示以及模型输出转换为数字标签。假设传入四个样本，它们的独热表示y_为（需要通过sess.run(y_)才能获取此Tensor的值，下同）：

1
2
3
4
[[1,0,0,0,0,0,0,0,0,0],
 [0,0,1,0,0,0,0,0,0,0],
 [0,0,0,0,0,0,0,0,0,1],
 [1,0,0,0,0,0,0,0,0,0]]

tf.argmax(y_,1)就是：

1
[0,2,9,0]

​ 也就是说，取出每一行最大值对应的下标位置，它们是输入样本的实际标签。假设此时模型的预测输出y为：

1
2
3
4
[[0.91,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01],
 [0.91,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01],
 [0.91,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01],
 [0.91,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01]]

tf.argmax(y_,1)就是：

1
[0,0,0,0]

​ 得到预测的标签和实际标签，接下来通过tf.equal函数来比较它们是否相等，并将结果保存到correct_prediction中。在上述例子中，correct_prediction就是：

1
[True,False,True,False]

        即第一个样本和最后一个样本预测是正确的，另外两个样本预测错误。可以用tf.cast(correct_prediction,tf.float32)将比较值转换成float32型的变量，此时True会被转换成1，False会被转换为0.在上述例子中，tf.cast(correct_prediction, tf.float32)的结果为：

1
[1.,0.,0.,1.]

        最后，用tf.reduce_mean可以计算数组中的所有元素的平均值，相当于得到了模型的预测准确率，如[1.,0.,0.,1.]的平均值为0,5，即50%的分类准确率。

        在程序softmax_regression.py中，传入占位符的值是feed_dict={x: mnist.test.images, y_: mnist.test.labels}。也就是说，使用全体测试样本进行测试，测试图片一共10000张，运行的结果为0.9052，即90.52%的准确率。因为softmax回归是一个比较简单的模型，这里的预测准确率并不高。

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import tensorflow as tf
# 导入MNIST教学的模块
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

# 创建x，x是一个占位符（placeholder），代表待识别的图片
x = tf.placeholder(tf.float32, [None, 784])
# W是Softmax模型的参数，将一个784维的输入转换为一个10维的输出
# 在TensorFlow中，变量的参数用tf.Variable表示
W = tf.Variable(tf.zeros([784, 10]))
# b是又一个Softmax模型的参数，我们一般叫做“偏置项”（bias）。
b = tf.Variable(tf.zeros([10]))

# y=softmax(Wx + b)，y表示模型的输出
y = tf.nn.softmax(tf.matmul(x, W) + b)
# y_是实际的图像标签，同样以占位符表示。
y_ = tf.placeholder(tf.float32, [None, 10])

# 至此，我们得到了两个重要的Tensor：y和y_。
# y是模型的输出，y_是实际的图像标签，不要忘了y_是独热表示的
# 下面我们就会根据y和y_构造损失

# 根据y, y_构造交叉熵损失
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y)))
# 有了损失，我们就可以用随机梯度下降针对模型的参数（W和b）进行优化
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

# 创建一个Session。只有在Session中才能运行优化步骤train_step。
sess = tf.InteractiveSession()
# 运行之前必须要初始化所有变量，分配内存。
tf.global_variables_initializer().run()
print('start training...')

# 进行1000步梯度下降
for _ in range(1000):
    # 在mnist.train中取100个训练数据
    # batch_xs是形状为(100, 784)的图像数据，batch_ys是形如(100, 10)的实际标签
    # batch_xs, batch_ys对应着两个占位符x和y_
    batch_xs, batch_ys = mnist.train.next_batch(100)
    # 在Session中运行train_step，运行时要传入占位符的值
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

# 正确的预测结果
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
# 计算预测准确率，它们都是Tensor
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 在Session中运行Tensor可以得到Tensor的值
# 这里是获取最终模型的正确率
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

本文标题:tensorflow入门笔记1

文章作者:goingcoder

发布时间:2018年05月14日 - 15:05

最后更新:2018年05月14日 - 19:05

原始链接:https://goingcoder.github.io/2018/05/14/tf9/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

-------------本文结束感谢您的阅读-------------