动态规划

发表于 |

​ 动态规划中递推式的求解方法不是动态规划的本质。 动态规划的本质，是对问题状态的定义和状态转移方程的定义。 动态规划是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。 本题下的其他答案，大多都是在说递推的求解方法，但如何拆分问题，才是动态规划的核心。 而拆分问题，靠的就是状态的定义和状态转移方程的定义。 要解决这个问题，我们首先要定义这个问题和这个问题的子问题。 有人可能会问了，题目都已经在这了，我们还需定义这个问题吗？需要，原因就是问题在字面上看，不容易找不出子问题，而没有子问题，这个题目就没办法解决 。状态转移方程，就是定义了问题和子问题之间的关系。 可以看出，状态转移方程就是带有条件的递推式。

一.阶乘(Factorial)

$1\times 2\times3\times\dots\times N$,整数1到$N$的连乘积。$N$阶乘$N!$

分析：$N!$源自$(N-1)!$，如此就递回分割问题了。

img

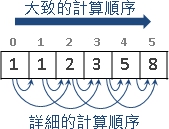
阵列的每一格对应每一个问题。设定第一格的答案，再以回圈依序计算其余答案。

img

1
2
3
4
5
6
7
8
9
const int N = 10;
int f[N];
void factorial()
{
    f[0] = 0;
    f[1] = 1;
    for (int i=2; i<=N; ++i)
        f[i] = f[i-1] * i;
}
1
2
3
4
5
6
7
8
const int N = 10;
 
void factorial()
{
    int f = 1;
    for (int i=2; i<=N; ++i)
        f *= i;
}

时间复杂度

总共$N$个问题，每个问题花费$O(1)$时间，总共花费$O(N)$时间

空间复杂度

求$1!$到$N!$:总共$N$个问题，用一条$N$格阵列存储全部问题的答案，空间复杂度为$O(N)$

只求$N!$:用一个变量累计成绩，空间复杂度为$O(1)$

Dynamic Programming: recurrence

Dynamic Programming = Divide and Conquer + Memoization

​ 动态规划是分治法的延伸。当递推分割出来的问题，一而再、再而三出现，就运用记忆法储存这些问题的答案，避免重复求解，以空间换取时间。动态规划的过程，就是反复地读取数据、计算数据、储存数据。

img

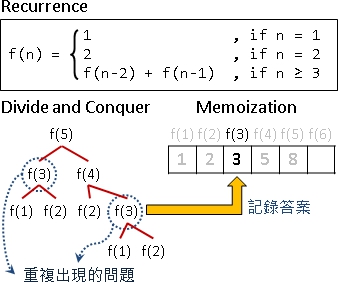
  1. 把原问题递归分割成许多更小的问题。（recurrence）

    子问题与原问题的求解方式皆类似。（optimal sub-structure）

    子问题会一而再、再而三的出现。（overlapping sub-problems）

  2. 设计计算过程：

    确认每个问题需要哪些子问题来计算答案。（recurrence）

    确认总共有哪些问题。（state space）

    把问题一一对应到表格。（lookup table）

    决定问题的计算顺序。（computational sequence）

​ 确认初始值、计算范围（initial states / boundary）

  1. 实作，主要有两种方式：

    Top-down

    Bottom-up

1. recurrence

​ 递归分割问题时，当子问题与原问题完全相同，只有数值范围不同，我们称此现象为recurrence，再度出现、一而再出现之意。

【注： recursion 和 recurrence ，中文都翻译为“递归”，然而两者意义大不相同，读者切莫混淆】

​ 此处以爬楼梯问题当做范例。先前于递归法章节，已经谈过如何求踏法，而此处要谈如何求踏法数目。

img

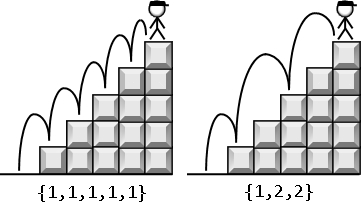
​ 踏上第五阶，只能从第四阶或从第三阶踏过去，因此爬到五阶源自两个子问题：爬到四阶与爬到三阶。

a

​ 爬到五阶的踏法数目，就是综合爬到四阶与爬到三阶的踏法数目。写成数学式子是$f(5)=f(4)+f(3)$，其中$f$表示爬到某阶的踏法数目。

​ 依样画葫芦，得到
$$
f(4)=f(3)+f(2)\\
f(3)=f(2)+f(1)
$$
​ 爬到两阶与爬到一阶无法再分割，没有子问题，直接得到
$$
f(2)=2\\
f(1)=1
$$
整理成一道简明扼要的递归公式：
$$
f(n)= \begin{cases}
1&if n=1 \\
2 & if n =2 \\
f(n-1)+f(n-2) & if n \ge3 and n\le 5
\end{cases}
$$
爬到任何一阶的踏法数目，都可以借由这道递归公式求得。img带入实际数值，递归计算即可。

​ 为什么分割问题之后，就容易计算答案呢？因为分割问题时，同时也分类了这个问题所有可能答案。分类使得答案的规律变得单纯，于是更容易求得答案。

img

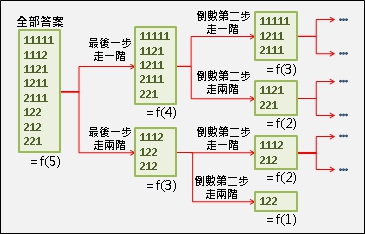
2 、state space

想要计算第五阶的踏法数目。

全部的问题是“爬到一节”、“爬到二阶”、“爬到三阶”、“爬到四阶”、“爬到五阶”。

img

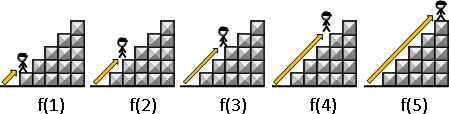
至于爬到零阶、爬到负一阶。爬到负二阶以及爬到六阶、爬到七阶没有必要计算。

3、lookup table

​ 建立六格的阵列，存储五个问题的答案。

​ 表格的第零格不使用，第一格式爬到一阶的答案，第二格是爬到二阶的答案，以此类推。

img

​ 如果只计算爬完五阶，也可以建立三个变量交替使用。

4、computational sequence

​ 因为每个问题都依赖阶数少一阶、阶数少两阶这两个问题，所以必须由阶数小的问题开始计算。

​ 计算顺序是爬到一阶、爬到二阶、……、爬到五阶。设定初始值。

5、 initial states / boundary

​ 最先计算的问题时爬到一阶与爬到二阶，必须预先将答案填入表格。写入方程式，才能计算其他问题。心算求得爬到一阶的答案是1，爬到二阶的答案是2。最后计算的问题时原问题是原问题爬到五阶。

​ 为了让表格更顺畅。为了让程式更漂亮，可以加入爬到零阶的答案，对应到表格的第零格。爬到零阶的答案，可以运用爬到一阶的答案与爬到两阶的答案，刻意逆推而得。

img

​ 最后可以把初始值，尚待计算的部分、不需计算的部分，整理成一道递归公式：
$$
f(n)= \begin{cases}
0 & if n<0\\ 0="" 1="" &="" if="" \="" n="0\\" 1&if="" \\="" f(n-1)+f(n-2)="" \ge2="" and="" n\le="" 5\\="">5
\end{cases}
$$

6、实现

​ 直接用递归实作，而不使用记忆体存储各个问题的答案，是最直接的方式，也是最慢的方式。时间复杂度是$O(f(n))$。问题一而再、再而三的出现，不断呼叫同样的函数求解，效率不彰。刚接触DP的新手常犯这种错误。

1
2
3
4
5
6
7
int f(int n)
{
    if (n == 0 || n == 1)
        return 1;
    else
        return f(n-1) + f(n-2);
}

​ 正确的DP是一边计算，一边将计算出来的数值存入表格，以便不必重算。这里整理了两种实现方式，各有优缺点。

1)Top-down

2)Bottom-up

img

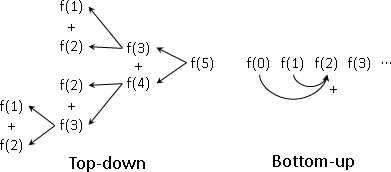
1)Top-down

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int table[6];   // 表格，储存全部问题的答案。
bool solve[6];  // 记录问题是否已经計算完毕
 
int f(int n)
{
    // [Initial]
    if (n == 0 || n == 1) return table[n] = 1;
 
    // [Compute]
    // 如果已經計算過，就直接讀取表格的答案。
    if (solve[n]) return table[n];
 
    // 如果不曾計算過，就計算一遍，儲存答案。
    table[n] = f(n-1) + f(n-2); // 將答案存入表格
    solve[n] = true;            // 已經計算完畢
    return table[n];
}
 
void stairs_climbing()
{
    for (int i=0; i<=5; i++)
        solve[i] = false;
 
    int n;
    while (cin >> n && (n >= 0 && n <= 5))
        cout << "爬到" << n << "阶，" << f(n) << "种踏法";
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int table[6];   // 合并solve跟table，简化代码。
int f(int n)
{
// [Initial]
    if (n == 0 || n == 1) return 1;

    // [Compute]
    // 用 0 代表该问题还未计算答案
//  if (table[n] != 0) 
return table[n];
if (table[n]) 
return table[n];
    return table[n] = f(n-1) + f(n-2);
}
 
void stairs_climbing()
{
   for (int i=0; i<=5; i++)
     table[i] = 0;
 
    int n;
    while (cin >> n && (n >= 0 && n <= 5))
        cout << "爬到" << n << "阶，" << f(n) << "种踏法";
}

​ 这个实现方式的好处是不必斤斤计较计算顺序，因为代码中的递归结构会迫使最小的问题先被计算。这个实现方式的另一个好处是只计算必要的问题，而不必计算所有可能的问题。

​ 这个实现的坏处是代码采用递归结构，不断调用函数，执行效率差。这个实现方式的另一个坏处是无法自由地控制计算顺序，因而无法妥善运用记忆体，浪费了可回收再利用的记忆体。

2）Bottom-up

​ 指定一个计算顺序，然后由最小问题开始计算。特色是代码通常只有几个递归。这个实现方式的好处与坏处与前一个方式恰好互补。

​ 首先建立表格。

1
2
int table[6];
int table[5 + 1];

心算爬到零阶的答案、爬到一阶的答案，填入报个当中，作为初始值。分别天道表格的第零格、第一格。

1
2
table[0] = 1;
table[1] = 1;

​ 尚待计算的部分就是爬到两阶的答案、……、爬到五阶的答案。通常是使用递归，按照计算顺序来计算。

计算过程的实现方式，有两种迥异的风格。一种是往回取值，是常见的实现方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
往回取值
int table[6];

void dynamic_programming()
{
    // [Initial]
    table[0] = 1;
    table[1] = 1;
 
    // [Compute]
    for (int i=2; i<=5; i++)
        table[i] = table[i-1] + table[i-2];
}

另一种是往后补值，是罕见的实现方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
往后补值int table[6];
 
void dynamic_programming()
{
    // [Initial]
    for (int i=0; i<=5; i++) table[i] = 0;
    table[0] = 1;
//  table[1] = 1;   // 剛好可以被算到
 
    // [Compute]
    for (int i=0; i<=5; i++)
    {
        if (i+1 <= 5) table[i+1] += table[i];
        if (i+2 <= 5) table[i+2] += table[i];
    }
}

7、总结

​ 第一，先找到原问题和其子问题之间的关系，写成递归公式。如此一来，即可利用递归公式，用子子问题的答案，求出子问题的答案；用子问题的答案，求出原问题的答案。

​ 第二。确认可能出现的问题全部总共有哪些；用子问题的答案，求出原问题的答案。

​ 第三。有了递归公式之后，就必须安排出一套计算顺序。大问题的答案，总是以小问题的答案来求得的，所以，小问题的答案必须是先算的，否则大问题的答案从何而来呢？一个好的安排方式，不但使代码易写，还可重复利用记忆体空间。

​ 第四。记得先将最小，最先被计算的问题，心算出答案，储存如表格，内建与代码之中。一道递归公式必须拥有初始值，才有计算其他项。

​ 第五。实现DP的代码时，会建立一个表格，表格存入所有大小问题的答案。安排好每个问题的答案再表格的哪个位置，这样计算时才能知道该在哪里取值。

​ 切勿存取超出表格的原始，产生溢位情形，导致答案算错。计算过程当中，一旦某个问题的答案出错，就会如骨牌效应般一个影响一个，造成很难除错。

-------------本文结束感谢您的阅读-------------