tf8

发表于 |

循环神经网络

​ 某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。比如，当我们在理解一句话意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；当我们处理视频的时候，我们也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。这时，就需要用到深度学习领域中另一类非常重要神经网络：循环神经网络(Recurrent Neural Network)。RNN种类很多，也比较绕脑子。不过读者不用担心，本文将一如既往的对复杂的东西剥茧抽丝，帮助您理解RNNs以及它的训练算法，并动手实现一个循环神经网络。

语言模型

​ RNN是在自然语言处理领域中最先被用起来的，比如，RNN可以为语言模型来建模。那么，什么是语言模型呢？我们可以和电脑玩一个游戏，我们写出一个句子前面的一些词，然后，让电脑帮我们写下接下来的一个词。比如下面这句：

我昨天上学迟到了，老师批评了__。

​ 我们给电脑展示了这句话前面这些词，然后，让电脑写下接下来的一个词。在这个例子中，接下来的这个词最有可能是『我』，而不太可能是『小明』，甚至是『吃饭』。

​ 语言模型就是这样的东西：给定一个一句话前面的部分，预测接下来最有可能的一个词是什么。

​ 语言模型是对一种语言的特征进行建模，它有很多很多用处。比如在语音转文本(STT)的应用中，声学模型输出的结果，往往是若干个可能的候选词，这时候就需要语言模型来从这些候选词中选择一个最可能的。当然，它同样也可以用在图像到文本的识别中(OCR)。

​ 使用RNN之前，语言模型主要是采用N-Gram。N可以是一个自然数，比如2或者3。它的含义是，假设一个词出现的概率只与前面N个词相关。我们以2-Gram为例。首先，对前面的一句话进行切词：

我 昨天 上学 迟到 了 ，老师 批评 了 。

​ 如果用2-Gram进行建模，那么电脑在预测的时候，只会看到前面的『了』，然后，电脑会在语料库中，搜索『了』后面最可能的一个词。不管最后电脑选的是不是『我』，我们都知道这个模型是不靠谱的，因为『了』前面说了那么一大堆实际上是没有用到的。如果是3-Gram模型呢，会搜索『批评了』后面最可能的词，感觉上比2-Gram靠谱了不少，但还是远远不够的。因为这句话最关键的信息『我』，远在9个词之前！

​ 现在读者可能会想，可以提升继续提升N的值呀，比如4-Gram、5-Gram…….。实际上，这个想法是没有实用性的。因为我们想处理任意长度的句子，N设为多少都不合适；另外，模型的大小和N的关系是指数级的，4-Gram模型就会占用海量的存储空间。

所以，该轮到RNN出场了，RNN理论上可以往前看(往后看)任意多个词。

循环神经网络是啥

循环神经网络种类繁多，我们先从最简单的基本循环神经网络开始吧。

基本循环神经网络

下图是一个简单的循环神经网络如，它由输入层、一个隐藏层和一个输出层组成：

1

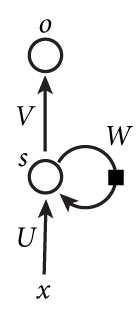
​ 纳尼？！相信第一次看到这个玩意的读者内心和我一样是崩溃的。因为循环神经网络实在是太难画出来了，网上所有大神们都不得不用了这种抽象艺术手法。不过，静下心来仔细看看的话，其实也是很好理解的。如果把上面有W的那个带箭头的圈去掉，它就变成了最普通的全连接神经网络。x是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）；s是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，你也可以想象这一层其实是多个节点，节点数与向量s的维度相同）；U是输入层到隐藏层的权重矩阵（读者可以回到第三篇文章零基础入门深度学习(3) - 神经网络和反向传播算法，看看我们是怎样用矩阵来表示全连接神经网络的计算的）；o也是一个向量，它表示输出层的值；V是隐藏层到输出层的权重矩阵。那么，现在我们来看看W是什么。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。输出层是一个全连接层，它的每个节点都和隐藏层的每个节点相连，隐藏层是循环层。

如果我们把上面的图展开，循环神经网络也可以画成下面这个样子：

2

​

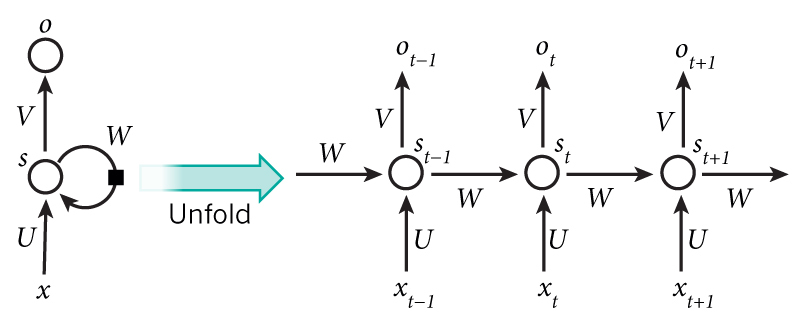
现在看上去就比较清楚了，这个网络在t时刻接收到输入$x_t$之后，隐藏层的值是$s_t$，输出值是$o_t$。关键一点是，$s_t$的值不仅仅取决于$x_t$，还取决于$s_{t-1}$。我们可以用下面的公式来表示循环神经网络的计算方法：
$$
o_t=g(Vs_t)…..(式1)……(1)\\
s_t=f(Ux_t+Ws_{t-1})…..(式2)……(2)
$$
​ 式1是输出层的计算公式，输出层是一个全连接层，也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵，g是激活函数。式2是隐藏层的计算公式，它是循环层。U是输入x的权重矩阵，W是上一次的值作为这一次的输入的权重矩阵，f是激活函数。

从上面的公式我们可以看出，循环层和全连接层的区别就是循环层多了一个权重矩阵 W。

如果反复把式2带入到式1，我们将得到：
$$
\begin{align}
\mathrm{o}_t&=g(V\mathrm{s}_t) ……….(3)\\
&=Vf(U\mathrm{x}_t+W\mathrm{s}_{t-1})…….(4)\\
&=Vf(U\mathrm{x}_t+Wf(U\mathrm{x}_{t-1}+W\mathrm{s}_{t-2}))……….(5)\\
&=Vf(U\mathrm{x}_t+Wf(U\mathrm{x}_{t-1}+Wf(U\mathrm{x}_{t-2}+W\mathrm{s}_{t-3})))……….(6)\\
&=Vf(U\mathrm{x}_t+Wf(U\mathrm{x}_{t-1}+Wf(U\mathrm{x}_{t-2}+Wf(U\mathrm{x}_{t-3}+…))))……….(7)
\end{align}
$$
从上面可以看出，循环神经网络的输出值$o_t$，是受前面历次输入值$x_t、x_{t-1}、x_{t-2}、x_{t-3}$…影响的，这就是为什么循环神经网络可以往前看任意多个输入值的原因。

双向循环神经网络

​ 对于语言模型来说，很多时候光看前面的词是不够的，比如下面这句话：

我的手机坏了，我打算____一部新手机。

​ 可以想象，如果我们只看横线前面的词，手机坏了，那么我是打算修一修？换一部新的？还是大哭一场？这些都是无法确定的。但如果我们也看到了横线后面的词是『一部新手机』，那么，横线上的词填『买』的概率就大得多了。

在上一小节中的基本循环神经网络是无法对此进行建模的，因此，我们需要双向循环神经网络，如下图所示：

3

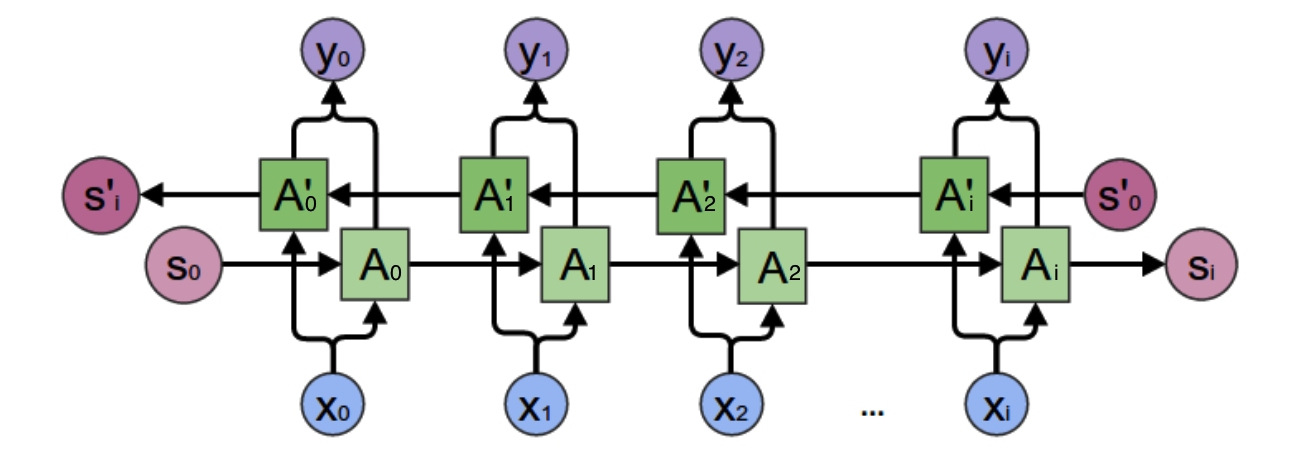
​ 当遇到这种从未来穿越回来的场景时，难免处于懵逼的状态。不过我们还是可以用屡试不爽的老办法：先分析一个特殊场景，然后再总结一般规律。我们先考虑上图中$y_2$的计算。

​ 从上图可以看出，双向卷积神经网络的隐藏层要保存两个值，一个A参与正向计算，另一个值A’参与反向计算。最终的输出值$y_2$取决于$A_2$和$A’_2$。其计算方法为：
$$
\mathrm{y}_2=g(VA_2+V’A_2’)
$$
$A_2$和$A’_2$则分别计算：
$$
\begin{align}
A_2&=f(WA_1+U\mathrm{x}_2)………(8)\\
A_2’&=f(W’A_3’+U’\mathrm{x}_2)…….(9)\\
\end{align}
$$
​ 现在，我们已经可以看出一般的规律：正向计算时，隐藏层的值$s_t$与$s_t-1$有关；反向计算时，隐藏层的值$s’_t$与$s’_{t-1}$有关；最终的输出取决于正向和反向计算的加和。现在，我们仿照式1和式2，写出双向循环神经网络的计算方法：
$$
\begin{align}
\mathrm{o}_t&=g(V\mathrm{s}_t+V’\mathrm{s}_t’)…….(10)\\
\mathrm{s}_t&=f(U\mathrm{x}_t+W\mathrm{s}_{t-1})…….(11)\\
\mathrm{s}_t’&=f(U’\mathrm{x}_t+W’\mathrm{s}_{t+1}’)……(12)\\
\end{align}
$$

​ 从上面三个公式我们可以看到，正向计算和反向计算不共享权重，也就是说U和U’、W和W’、V和V’都是不同的权重矩阵。

深度循环神经网络

前面我们介绍的循环神经网络只有一个隐藏层，我们当然也可以堆叠两个以上的隐藏层，这样就得到了深度循环神经网络。如下图所示：

4

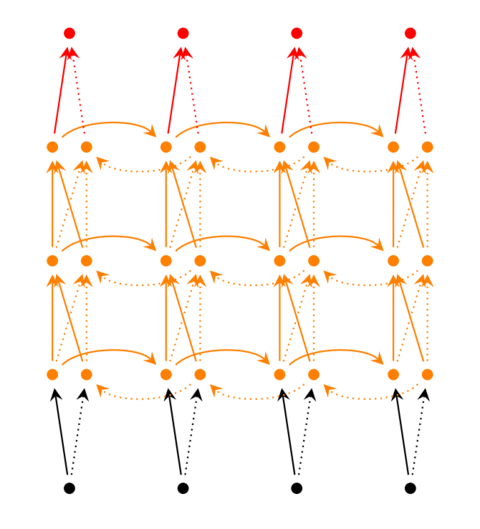
我们把第i个隐藏层的值表示为$s_t^{(i)}$、$s_t^{‘(i)}$，则深度循环神经网络的计算方式可以表示为：
$$
\begin{align}
\mathrm{o}_t&=g(V^{(i)}\mathrm{s}_t^{(i)}+V’^{(i)}\mathrm{s}_t’^{(i)})…….(13)\\
\mathrm{s}_t^{(i)}&=f(U^{(i)}\mathrm{s}_t^{(i-1)}+W^{(i)}\mathrm{s}_{t-1})……….(14)\\
\mathrm{s}_t’^{(i)}&=f(U’^{(i)}\mathrm{s}_t’^{(i-1)}+W’^{(i)}\mathrm{s}_{t+1}’)……..(15)\\
…(16)\\
\mathrm{s}_t^{(1)}&=f(U^{(1)}\mathrm{x}_t+W^{(1)}\mathrm{s}_{t-1})……..(17)\\
\mathrm{s}_t’^{(1)}&=f(U’^{(1)}\mathrm{x}_t+W’^{(1)}\mathrm{s}_{t+1}’)………(18)\\
\end{align}
$$

循环神经网络的训练

循环神经网络的训练算法：BPTT

BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤：

  1. 前向计算每个神经元的输出值；
  2. 反向计算每个神经元的误差项$\delta_j$值，它是误差函数E对神经元j的加权输入$net_j$的偏导数；
  3. 计算每个权重的梯度。

最后再用随机梯度下降算法更新权重。

循环层如下图所示：

5

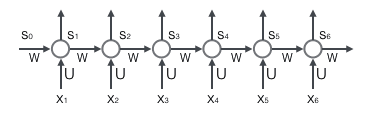
前向计算

使用前面的式2对循环层进行前向计算：
$$
\mathrm{s}_t=f(U\mathrm{x}_t+W\mathrm{s}_{t-1})
$$
注意，上面的$s_t$、$x_t$、$s_{t-1}$都是向量，用黑体字母表示；而U、V是矩阵，用大写字母表示。向量的下标表示时刻，例如，表示在t时刻向量s的值。

​ 我们假设输入向量x的维度是m，输出向量s的维度是n，则矩阵U的维度是$n m$，矩阵W的维度是$nn$。下面是上式展开成矩阵的样子，看起来更直观一些：
$$
\begin{align}
\begin{bmatrix}
s_1^t\\
s_2^t\\
.\.\\
s_n^t\\
\end{bmatrix}=f(
\begin{bmatrix}
u_{11} u_{12} … u_{1m}\\
u_{21} u_{22} … u_{2m}\\
.\.\\
u_{n1} u_{n2} … u_{nm}\\
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
.\.\\
x_m\\
\end{bmatrix}+
\begin{bmatrix}
w_{11} w_{12} … w_{1n}\\
w_{21} w_{22} … w_{2n}\\
.\.\\
w_{n1} w_{n2} … w_{nn}\\
\end{bmatrix}
\begin{bmatrix}
s_1^{t-1}\\
s_2^{t-1}\\
.\.\\
s_n^{t-1}\\
\end{bmatrix})…..(19)
\end{align}
$$
​ 在这里我们用手写体字母表示向量的一个元素，它的下标表示它是这个向量的第几个元素，它的上标表示第几个时刻。例如，$s_t^{j}$表示向量s的第j个元素在t时刻的值。$u_{ji}$表示输入层第i个神经元到循环层第j个神经元的权重。$w_{ji}$表示循环层第t-1时刻的第i个神经元到循环层第t个时刻的第j个神经元的权重。

误差项的计算

​ BTPP算法将第l层t时刻的误差项$\delta_t^l $值沿两个方向传播，一个方向是其传递到上一层网络，得到，这部分只和权重矩阵U有关；另一个是方向是将其沿时间线传递到初始时刻，得到，这部分只和权重矩阵W有关。

我们用向量表示神经元在t时刻的加权输入，因为：

6

其中，$X_t$为输入，A为模型处理部分，$h_t$为输出。

为了更容易地说明递归神经网络，我们把上图展开，得到：

7

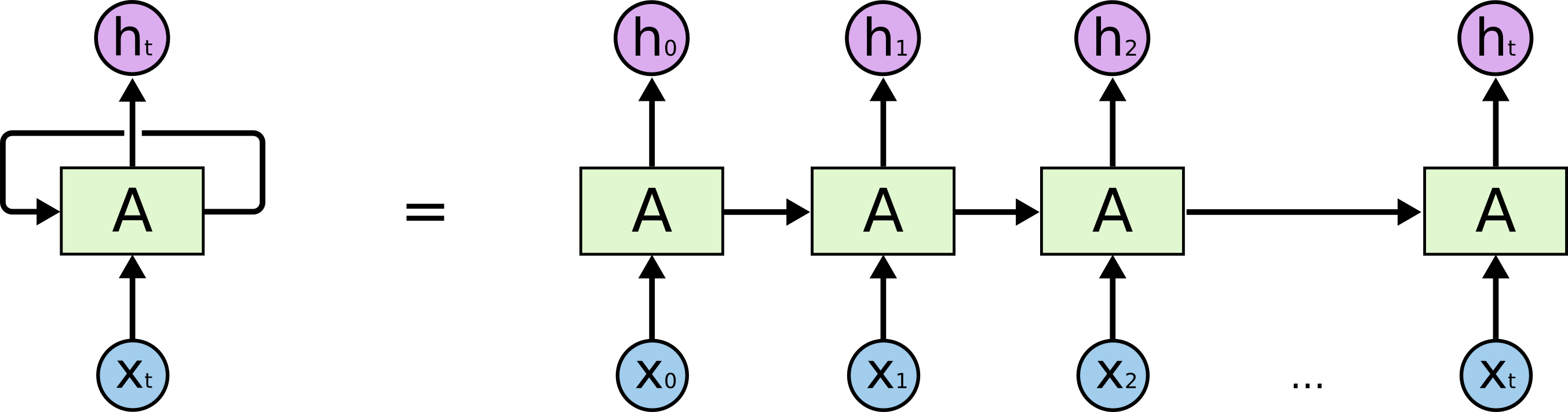
​ 这样的一条链状神经网络代表了一个递归神经网络，可以认为它是对相同神经网络的多重复制，每一时刻的神经网络会传递信息给下一时刻。如何理解它呢？假设有这样一个语言模型，我们要根据句子中已出现的词预测当前词是什么，递归神经网络的工作原理如下：

8

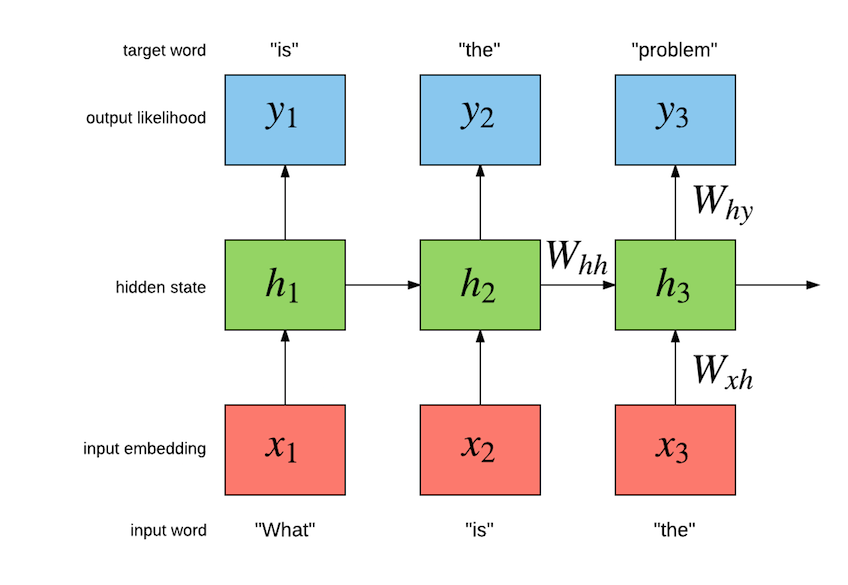
其中，W为各类权重，x表示输入，y表示输出，h表示隐层处理状态。

递归神经网络因为具有一定的记忆功能，可以被用来解决很多问题，例如：语音识别、语言模型、机器翻译等。但是它并不能很好地处理长时依赖问题。

长时依赖问题

​ RNN 的关键点之一就是他们可以用来连接先前的信息到当前的任务上，例如使用过去的视频段来推测对当前段的理解。如果 RNN 可以做到这个，他们就变得非常有用。但是真的可以么？答案是，还有很多依赖因素。

​ 有时候，我们仅仅需要知道先前的信息来执行当前的任务。例如，我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the sky” 最后的词，我们并不需要任何其他的上下文 —— 因此下一个词很显然就应该是 sky。在这样的场景中，相关的信息和预测的词位置之间的间隔是非常小的，RNN 可以学会使用先前的信息。

9

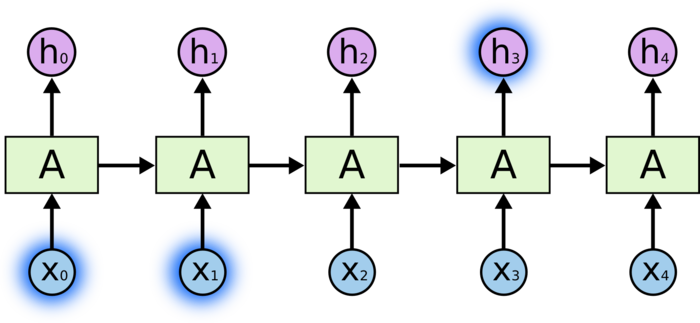
​ 不太长的相关信息和位置间隔

​ 但是同样会有一些更加复杂的场景。假设我们试着去预测“I grew up in France… I speak fluent French”最后的词。当前的信息建议下一个词可能是一种语言的名字，但是如果我们需要弄清楚是什么语言，我们是需要先前提到的离当前位置很远的 France 的上下文的。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。

​ 不幸的是，在这个间隔不断增大时，RNN 会丧失学习到连接如此远的信息的能力。

10

​ 在理论上，RNN 绝对可以处理这样的 长期依赖 问题。人们可以仔细挑选参数来解决这类问题中的最初级形式，但在实践中，RNN 肯定不能够成功学习到这些知识。Bengio, et al. (1994)等人对该问题进行了深入的研究，他们发现一些使训练 RNN 变得非常困难的相当根本的原因。

​ 隐含内容和输出结果是相同的内容。

​ TensorFlow 实现 RNN Cell 的位置在 python/ops/rnn_cell_impl.py，首先其实现了一个 RNNCell 类，继承了 Layer 类，其内部有三个比较重要的方法，state_size()、output_size()、call() 方法，其中 state_size() 和 output_size() 方法设置为类属性，可以当做属性来调用，实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
@property
def state_size(self):
"""size(s) of state(s) used by this cell.
It can be represented by an Integer, a TensorShape or a tuple of Integers
or TensorShapes.
"""
    raise NotImplementedError("Abstract method")

@property
def output_size(self):
"""Integer or TensorShape: size of outputs produced by this cell."""
    raise NotImplementedError("Abstract method")

分别代表 Cell 的状态和输出维度，和 Cell 中的神经元数量有关，但这里两个方法都没有实现，意思是说我们必须要实现一个子类继承 RNNCell 类并实现这两个方法。

另外对于 call() 方法，实际上就是当初始化的对象直接被调用的时候触发的方法，实现如下：

1
2
3
4
5
6
7
8
9
def __call__(self, inputs, state, scope=None):
    if scope is not None:
        with vs.variable_scope(scope,
                               custom_getter=self._rnn_get_variable) as scope:
            return super(RNNCell, self).__call__(inputs, state, scope=scope)
    else:
        with vs.variable_scope(vs.get_variable_scope(),
                               custom_getter=self._rnn_get_variable):
            return super(RNNCell, self).__call__(inputs, state)

​ 实际上是调用了父类 Layer 的 call() 方法，但父类中 call() 方法中又调用了 call() 方法，而 Layer 类的 call() 方法的实现如下：

1
2
def call(self, inputs, **kwargs):
    return inputs

父类的 call() 方法实现非常简单，所以要实现其真正的功能，只需要在继承 RNNCell 类的子类中实现 call() 方法即可。

接下来我们看下 RNN Cell 的最基本的实现，叫做 BasicRNNCell，其代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class BasicRNNCell(RNNCell):
  """The most basic RNN cell.
  Args:
    num_units: int, The number of units in the RNN cell.
    activation: Nonlinearity to use.  Default: `tanh`.
    reuse: (optional) Python boolean describing whether to reuse variables
     in an existing scope.  If not `True`, and the existing scope already has
     the given variables, an error is raised.
  """

  def __init__(self, num_units, activation=None, reuse=None):
    super(BasicRNNCell, self).__init__(_reuse=reuse)
    self._num_units = num_units
    self._activation = activation or math_ops.tanh
    self._linear = None

  @property
  def state_size(self):
    return self._num_units

  @property
  def output_size(self):
    return self._num_units

  def call(self, inputs, state):
    """Most basic RNN: output = new_state = act(W * input + U * state + B)."""
    if self._linear is None:
      self._linear = _Linear([inputs, state], self._num_units, True)

    output = self._activation(self._linear([inputs, state]))
    return output, output

可以看到在初始化的时候，最重要的一个参数是 num_units，意思就是这个 Cell 中神经元的个数，另外还有一个参数 activation 即默认使用的激活函数，默认使用的 tanh，reuse 代表该 Cell 是否可以被重新使用。

在 state_size()、output_size() 方法里，其返回的内容都是 num_units，即神经元的个数，接下来 call() 方法中，传入的参数为 inputs 和 state，即输入的 x 和 上一次的隐含状态，首先实例化了一个 _Linear 类，这个类实际上就是做线性变换的类，将二者传递过来，然后直接调用，就实现了 w * [inputs, state] + b 的线性变换，其中 _Linear 类的 call() 方法实现如下：

1
2
3
4
5
6
7
8
9
10
def __call__(self, args):
    if not self._is_sequence:
        args = [args]
    if len(args) == 1:
        res = math_ops.matmul(args[0], self._weights)
    else:
        res = math_ops.matmul(array_ops.concat(args, 1), self._weights)
    if self._build_bias:
        res = nn_ops.bias_add(res, self._biases)
    return res

​ 很明显这里传递了 [inputs, state] 作为 call() 方法的 args，会执行 concat() 和 matmul() 方法，然后接着再执行 bias_add() 方法，这样就实现了线性变换。

​ 最后回到 BasicRNNCell 的 call() 方法中，在 _linear() 方法外面又包括了一层 _activation() 方法，即对线性变换应用一次 tanh 激活函数处理，作为输出结果。

​ 最后返回的结果是 output 和 output，第一个代表 output，第二个代表隐状态，其值也等于 output。

-------------本文结束感谢您的阅读-------------