线性单元
感知器有一个问题,当面对的数据集不是线性可分的时候,『感知器规则』可能无法收敛,这意味着我们永远也无法完成一个感知器的训练。为了解决这个问题,我们使用一个可导的线性函数来替代感知器的阶跃函数,这种感知器就叫做线性单元。线性单元在面对线性不可分的数据集时,会收敛到一个最佳的近似上。
为了简单起见,我们可以设置线性单元的激活函数$f$为
$f(x)=x$
这样的线性单元如下图所示
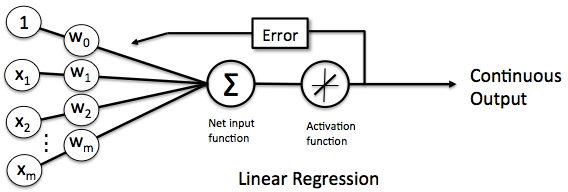
感知器
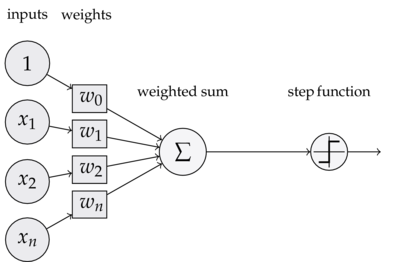
替换激活函数之后,线性单元将返回一个实数值而不是0,1分类。因此线性单元用来解决回归问题而不是分类问题。
线性单元的模型
当我们说模型时,我们实际上在谈论根据输入$x$预测输出$y$的算法。比如,$x$可以是一个人的工作年限,$y$可以是他的月薪,我们可以用某种算法来根据一个人的工作年限来预测他的收入。比如:
$y=h(x)=w*x+b$
函数$h(x)$叫做假设,而$w,b$是它的参数。我们假设参数$w=1000$,参数$b=500$,如果一个人的工作年限是5年的话,我们的模型会预测他的月薪为
$y=h(x)=1000*5+500=5500(元)$
你也许会说,这个模型太不靠谱了。是这样的,因为我们考虑的因素太少了,仅仅包含了工作年限。如果考虑更多的因素,比如所处的行业、公司、职级等等,可能预测就会靠谱的多。我们把工作年限、行业、公司、职级这些信息,称之为特征。对于一个工作了5年,在IT行业,百度工作,职级T6这样的人,我们可以用这样的一个特征向量来表示他
$x=(5,IT,百度,T6)$
既然输入$x$变成了一个具备四个特征的向量,相对应的,仅仅一个参数$w$就不够用了,我们应该使用4个参数$w_1,w_2,w_3,w_4$,每个特征对应一个。这样,我们的模型就变成
$y=h(x)=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b$
其中,$x_1$对应工作年限,$x_2$对应行业,$x_3$对应公司,$x_4$对应职称。
为了书写和计算方便,我们可以$w_0$令等于$b$,同时令$w_0$对应于特征$x_0$。由于$x_0$其实并不存在,我们可以令它的值永远为1。也就是说
$b=w_0*x_0$ 其中$x_0=1$
这样上面的式子就可以写成
$y=h(x)=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b$ ………….(1)
$=w_0x_0+w_1x_1+w_2x_2+w_3x_3+w_4*x_4$ ………….(2)
我们还可以把上式写成向量的形式
$y=h(x)=w^Tx$
长成这种样子模型就叫做线性模型,因为输出$y$就是输入特征$x_1,x_2,x_3,…$的线性组合。
监督学习和无监督学习
接下来,我们需要关心的是这个模型如何训练,也就是参数$w$取什么值最合适。
机器学习有一类学习方法叫做监督学习,它是说为了训练一个模型,我们要提供这样一堆训练样本:每个训练样本既包括输入特征$x$,也包括对应的输出$y$(也叫做标记,label)。也就是说,我们要找到很多人,我们既知道他们的特征(工作年限,行业…),也知道他们的收入。我们用这样的样本去训练模型,让模型既看到我们提出的每个问题(输入特征),也看到对应问题的答案(标记)。当模型看到足够多的样本之后,它就能总结出其中的一些规律。然后,就可以预测那些它没看过的输入所对应的答案了。
另外一类学习方法叫做无监督学习,这种方法的训练样本中只有而没有。模型可以总结出特征的一些规律,但是无法知道其对应的答案$y$。
很多时候,既有$x$又有的$y$训练样本是很少的,大部分样本都只有$x$。比如在语音到文本(STT)的识别任务中,$x$是语音,$y$是这段语音对应的文本。我们很容易获取大量的语音录音,然而把语音一段一段切分好并标注上对应文字则是非常费力气的事情。这种情况下,为了弥补带标注样本的不足,我们可以用无监督学习方法先做一些聚类,让模型总结出哪些音节是相似的,然后再用少量的带标注的训练样本,告诉模型其中一些音节对应的文字。这样模型就可以把相似的音节都对应到相应文字上,完成模型的训练。
线性单元的目标函数
现在,让我们只考虑监督学习。
在监督学习下,对于一个样本,我们知道它的特征$x$,以及标记$y$。同时,我们还可以根据模型计算得到输出。注意这里面我们用表示训练样本里面的标记,也就是实际值;用带上划线的表示模型计算的出来的预测值。我们当然希望模型计算出来的和越接近越好。
数学上有很多方法来表示的$\overline y$和$y$的接近程度,比如我们可以用$\overline y$和$y$的差的平方的$1\over2$来表示它们的接近程度
$e={1\over2}(y-\overline y)^2$
我们把$e$叫做单个样本的误差。至于为什么前面要乘$1\over 2$,是为了后面计算方便。
训练数据中会有很多样本,比如$N$个,我们可以用训练数据中所有样本的误差的和,来表示模型的误差$E$,也就是$E=e^{(1)}+e^{(2)}+e^{(3)}+\dots+e^{(n)}$
上式的$e^{(1)}$表示第一个样本的误差,$e^{(2)}$表示第二个样本的误差……。
我们还可以把上面的式子写成和式的形式。使用和式,不光书写起来简单,逼格也跟着暴涨,一举两得。所以一定要写成下面这样
$E=e^{(1)}+e^{(2)}+e^{(3)}+\dots+e^{(n)}$ …………………(3)
$\sum_{i=1}^n e^{(i)} $ …………………(4)
$={1\over 2}\sum_{i=1}^n(y^(i)-\overline y^{(i)})^2$ . …………………(5)
其中
$\overline y^{(i)}=h(x^{(i)})$ ……………………..(6)
$=w^Tx^{(i)}$ ………………………..(7)
(5)中,$x^{(i)}$表示第$i$个训练样本的特征,$y^{(i)}$表示第$i$个样本的标记,我们也可以用元组$(x^{(i)},y^{(i)})$表示第$i$个 训练样本。$\overline y^{(i)}$则是模型对第$i$个样本的预测值。
我们当然希望对于一个训练数据集来说,误差最小越好,也就是(5)的值越小越好。对于特定的训练数据集来说,$(x^{(i)},y^{(i)})$的值都是已知的,所以(式2)其实是参数$w$的函数。
$E(w)={1\over 2}\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})^2 $ ……………………..(8)
$={1\over 2}\sum_{i=1}^n(y^{(i)}-w^Tx^{(i)})^2$ ………………………….(9)
由此可见,模型的训练,实际上就是求取到合适的,使(5)取得最小值。这在数学上称作优化问题,而就是我们优化的目标,称之为目标函数。
梯度下降优化算法
我们学过怎样求函数的极值。函数$y=f(x)$的极值点,就是它的导数$f’(x)=0$的那个点。因此我们可以通过解方程$f’(x)=0$,求得函数的极值点$(x_0,y_0)$。
不过对于计算机来说,它可不会解方程。但是它可以凭借强大的计算能力,一步一步的去把函数的极值点『试』出来。如下图所示:
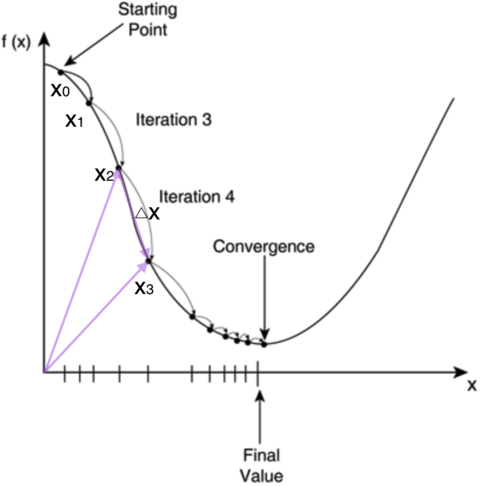
首先,我们随便选择一个点开始,比如上图的点$x_0$。接下来,每次迭代修改$x$的为,经过数次迭代后最终达到函数最小值点。
你可能要问了,为啥每次修改的值,都能往函数最小值那个方向前进呢?这里的奥秘在于,我们每次都是向函数$y=f(x)$的梯度的相反方向来修改$x$。什么是梯度呢?梯度是一个向量,它指向函数值上升最快的方向。显然,梯度的反方向当然就是函数值下降最快的方向了。我们每次沿着梯度相反方向去修改的值,当然就能走到函数的最小值附近。之所以是最小值附近而不是最小值那个点,是因为我们每次移动的步长不会那么恰到好处,有可能最后一次迭代走远了越过了最小值那个点。步长的选择是门手艺,如果选择小了,那么就会迭代很多轮才能走到最小值附近;如果选择大了,那可能就会越过最小值很远,收敛不到一个好的点上。
按照上面的讨论,我们就可以写出梯度下降算法的公式
$x_{new}=x_{old}-\eta\nabla f(x)$
其中,$\nabla$是梯度算子,$\nabla f(x)$就是指的梯度。$\eta$是步长,也称作学习速率。
对于上一节列出的目标函数(式5)
$E(w)={1\over2}\sum_{i=1}^n(y^{(i)}-\overline y^{(i)}$
梯度下降算法可以写成
$w_{new}=w_{old}+\eta\nabla E(w)$
我们要来求取$\nabla E(w)$,然后带入上式,就能得到线性单元的参数修改规则。
关于$\nabla E(w)$的推导过程,我单独把它们放到一节中。您既可以选择慢慢看,也可以选择无视。在这里,您只需要知道,经过一大串推导,目标函数$E(w)$的梯度是
$\nabla E(w)=-\sum_{i=1}^{n}(y^{(i)}-\overline y^{(i)})x^{(i)}$
因此,线性单元的参数修改规则最后是这个样子
$w_{new}=w_{old}+\eta\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})$
有了上面这个式子,我们就可以根据它来写出训练线性单元的代码了。
需要说明的是,如果每个样本有M个特征,则上式w,x都是M+1维向量(因为我们加上了一个恒为1的虚拟特征$x_0$,参考前面的内容),而$y$是标量。用高逼格的数学符号表示 ,就是
$w,x\in R^{(M+1)}$
$y\in R^1$
为了让您看明白说的是啥,我吐血写下下面这个解释(写这种公式可累可累了)。因为$w,x$是M+1维列向量,所以(式3)可以写成
$$
\begin{bmatrix}
w_0 \\
w_1\\
w_2\\
\dots\\
w_m\\
\end{bmatrix}=\begin{bmatrix}
w_0 \\
w_1\\
w_2\\
\dots\\
w_m\\
\end{bmatrix}+\eta\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})\begin{bmatrix}
1 \\
x_1^{(i)}\\
x_2^{(i)}\\
\dots\\
x_m^{(i)}\\
\end{bmatrix}
$$
$\nabla E(w)$的推导
这一节你尽可以跳过它,并不太会影响到全文的理解。当然如果你非要弄明白每个细节,那恭喜你骚年,机器学习的未来一定是属于你的。
首先,我们先做一个简单的前戏。我们知道函数的梯度的定义就是它相对于各个变量的偏导数,所以我们写下下面的式子
$$
\nabla E(w)={\partial\over\partial w}E(w) …………….(10)\\
={\partial\over \partial w}{1\over2}\sum_{i=1}^n(y^{(i)} - \overline y^{(i)})………….(11)
$$
可接下来怎么办呢?我们知道和的导数等于导数的和,所以我们可以先把求和符号$\sum$里面的导数求出来,然后再把它们加在一起就行了,也就是
$$
{\partial \over \partial w }{1\over 2}\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})^2…………(12)\\
={1\over 2}\sum_{i=1}^n{\partial\over \partial w}(y^{(i)}-\overline y^{(i)})^2…………(13)
$$
现在我们可以不管高大上的$\sum$了,先专心把里面的导数求出来。
$$
{\partial \over \partial w}(y^{(i)}-\overline y^{(i)})^2………………….(14)\\
={\partial \over \partial w}({y^{(i)}}^2-2\overline y^{(i)} +{\overline y^{(i)}}^2)………………….(15)
$$
我们知道,$y$是与$w$无关的常数,而$\overline y=w^Tx$,下面我们根据链式求导法则来求导。
$$
{\partial E(w)\over \partial w}={\partial E(\overline y)\over \partial\overline y}{\partial\overline y\over \partial w}
$$
我们分别计算上式等号右边的两个偏导数
$$
{\partial E(w)\over \partial \overline y}={\partial \over\partial \overline y}({y^{(i)}}^2-2\overline y^{(i)}y^{(i)}+{\overline y^{(i)}}^2)…………(16)\\
=-2y^{(i)}+2\overline y ^{(i)}……………….(17)
$$
$$
{\partial \overline y \over \partial w}={\partial \over\partial w}w^Tx ……………………..(18)\\
=x……………………(19)
$$
代入,我们求得$\sum$里面的偏导数是
$$
{\partial \over \partial w}(y^{(i)}-\overline y^{(i)})^2………………………..(20)\\
=2(-y^{(i)}+\overline y^{(i)})x……………………….(21)
$$
最后代入$\nabla E(w)$,求得
$$
\nabla E(w)={1\over2}\sum_{i=1}^n{\partial\over \partial w}(y^{(i)}-\overline y^{(i)})^2…………..(22)\\
={1\over 2}\sum_{i=1}^n2(-y^{(i)}+\overline y^{(i)})x…………….(23)\\
=-\sum_{i=1}^n(y^{(i)}-\overline y^{(i)})x……………….(25)
$$
随机梯度下降算法(Stochastic Gradient Descent, SGD)
如果我们根据上面式子来训练模型,那么我们每次更新的迭代,要遍历训练数据中所有的样本进行计算,我们称这种算法叫做批梯度下降(Batch Gradient Descent)。如果我们的样本非常大,比如数百万到数亿,那么计算量异常巨大。因此,实用的算法是SGD算法。在SGD算法中,每次更新的迭代,只计算一个样本。这样对于一个具有数百万样本的训练数据,完成一次遍历就会对更新数百万次,效率大大提升。由于样本的噪音和随机性,每次更新并不一定按照减少的方向。然而,虽然存在一定随机性,大量的更新总体上沿着减少的方向前进的,因此最后也能收敛到最小值附近。下图展示了SGD和BGD的区别
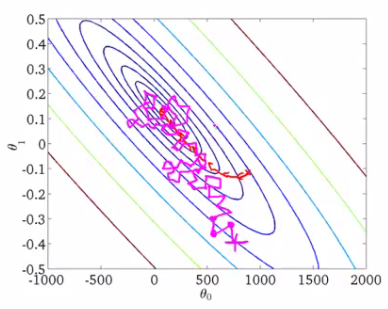
如上图,椭圆表示的是函数值的等高线,椭圆中心是函数的最小值点。红色是BGD的逼近曲线,而紫色是SGD的逼近曲线。我们可以看到BGD是一直向着最低点前进的,而SGD明显躁动了许多,但总体上仍然是向最低点逼近的。
最后需要说明的是,SGD不仅仅效率高,而且随机性有时候反而是好事。今天的目标函数是一个『凸函数』,沿着梯度反方向就能找到全局唯一的最小值。然而对于非凸函数来说,存在许多局部最小值。随机性有助于我们逃离某些很糟糕的局部最小值,从而获得一个更好的模型。
小结
事实上,一个机器学习算法其实只有两部分
模型 从输入特征预测输入的那个函数
目标函数 目标函数取最小(最大)值时所对应的参数值,就是模型的参数的最优值。很多时候我们只能获得目标函数的局部最小(最大)值,因此也只能得到模型参数的局部最优值。
因此,如果你想最简洁的介绍一个算法,列出这两个函数就行了。
接下来,你会用优化算法去求取目标函数的最小(最大)值。[随机]梯度{下降|上升}算法就是一个优化算法。针对同一个目标函数,不同的优化算法会推导出不同的训练规则。我们后面还会讲其它的优化算法。
其实在机器学习中,算法往往并不是关键,真正的关键之处在于选取特征。选取特征需要我们人类对问题的深刻理解,经验、以及思考。而神经网络算法的一个优势,就在于它能够自动学习到应该提取什么特征,从而使算法不再那么依赖人类,而这也是神经网络之所以吸引人的一个方面。
现在,经过漫长的烧脑,你已经具备了学习神经网络的必备知识。下一篇文章,我们将介绍本系列文章的主角:神经网络,以及用来训练神经网络的大名鼎鼎的算法:反向传播算法。至于现在,我们应该暂时忘记一切,尽情奖励自己一下吧。