逻辑斯谛分布
首先介绍逻辑斯谛分布,该分布的定义是
设$X$是连续随机变量,$X$服从逻辑斯谛分布是指$X$ 服从如下分布函数和密度函数:
$F(x)=P(X\le x)={1\over 1+e^{-(x-\mu)}/\gamma}$ …………..(1)
$f(x)=F^,(X\le x)={e^{-(x-\mu)/\gamma}\over \gamma(1+e^{-(x-\mu)/\gamma})}$ …………(2)
式中,$\mu$为位置参数 ,$\gamma>0$ 为形状参数。
逻辑斯蒂分布的密度函数$f(x)$ 和分布函数$F(x)$的图形如下图所示。
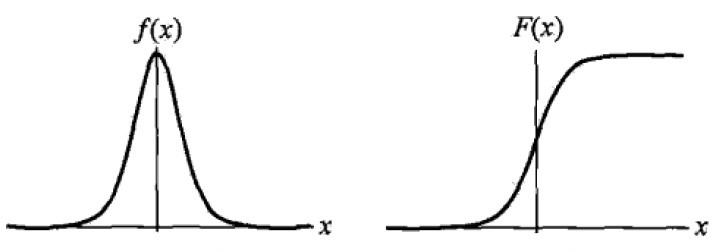
分布函数属于逻辑斯蒂函数,其图形是一条$S$形曲线(sigmoid curve).该曲线以点$(\mu,{1 \over 2})$为中心对称,即满足
$F(-x+\mu)-{1\over 2}=-F(x+\mu)+{1\over 2}$
曲线在中心附近增长速度较快,在两端增长速度较慢。形状参数$\gamma$ 的值越小,曲线在中心附近增长越快。
二项逻辑斯蒂回归模型
二项逻辑回归模型(binomial logistic regression model)是一种分类模型,由条件概率分布$P(Y|X)$ 表示,形式为参数化的逻辑斯蒂分布。这里,随机变量$X$ 取值为实数,随机变量$Y$取值为1或0。我们通过监督学习的方法来估计模型参数。
这是一种由条件概率表示的模型,其条件概率模型如下:
$P(Y=1|x)={exp(w \cdot x +b) \over 1+exp(w \cdot x +b)}$ ………….(3)
$P(Y=0|x)={1 \over 1+exp(w \cdot x +b)}$ ………….(4)
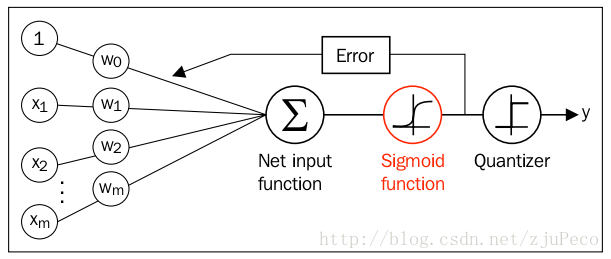
图 逻辑回归网络
这里,$x\in R^n$ 是输入,$Y \in{0,1}$是输出,$w\in R^n$和$b\in R$是参数,$w$称为权重向量,$b$称为偏置,$w\cdot x$为$w$和$x$的內积。
对于给定的输入实例$x$,按照(3)和(4)可以求得$P(Y=1|x)$和$P(Y=0|x)$。逻辑斯蒂回归比较两个条件概率值得大小,将实例$x$分到概率值较大的那一类。 有时为了方便,将权值向量和输入向量加以扩充,仍记作$w$,$x$,即$w=(w^{(1)},w^{(2)},\dots,w^{n},b) ^T$,$x=(x^{(1)},x^{(2)},\dots,x^{(n)},1)^T$ 。这时,逻辑斯蒂回归模型如下:
$P(Y=1|x)={exp(w \cdot x) \over 1+exp(w \cdot x)}$ ………..(5)
$P(Y=0|x)={1 \over 1+exp(w \cdot x)}$ ………..(6)
其实分子分母同时除以指数部分,就变成sigmoid函数了。
现在考查逻辑斯蒂回归模型的特点。一个时间的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是$p$,那么该事件的几率是$p\over{1-p}$,该事件的对数几率(log odds)或者logit函数是
$logit(p)=log{p\over{1-p}}$
对逻辑斯蒂回归而言,由式(5)与(6)得
$log{P(Y=1|x)\over {1-P(Y=1|x)}}=w \cdot x$
这就是说,在逻辑斯蒂回归模型中,输出$Y=1$的对数几率是输入$x$的线性函数。或者说输出$Y=1$的对数几率是由输入$x$的线性函数表示的模型,即逻辑斯蒂回归模型。反过来讲,如果知道权值向量,给定输入$x$,就能求出$Y=1$的概率:
注意 ,这里$x\in R^{n+1},w\in R^{n+1}$。通过逻辑斯蒂回归模型定义式(5)可以将线性函数$w\cdot x$转换为概率:
$P(Y=1|x)={exp(w\cdot x)\over{1+exp(w\cdot x)}}$
这时,线性函数的值越接近正无穷,概率值就越接近1;线性函数的值越接近无穷,概率值就越接近0。这样的模型就是逻辑斯蒂回归模型。
模型参数估计
根据给定的数据集,把参数$w$给求出来了。要找参数$w$,首先就是得把代价函数给定义出来,也就是目标函数。首先想到的是类型线性回归的做法,利用误差平方来当代价函数。
$J(w)=\sum_{i}{1\over 2}(\phi(z^{i})-y^i)^2$
其中 $z^i=w\cdot x$ ,$i$表示第$i$个样本点,$y^i$表示第$i$个样本的真实值,$\phi(z^{i})$表示第$i$个样本的预测值 。
$\phi(z^{i}) ={1\over 1+e^{-z^i}}$ ,这是一个非凸函数,这就意味着代价函数有着许多的局部最小值,不利于我们的求解。
逻辑斯蒂回归模型学习中,对于给定的训练数据集$T={(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)}$,其中,$x_i\in R^n,y_i\in{0,1}$可以应用极大似然估计法估计模型参数,从而得到逻辑斯蒂回归模型。
设:
$P(Y=1|x)=\pi(x)$
$P(Y=0|x)=1-\pi(x)$
对于每一个观察到的样本$(x_i,y_i)$ 出现的概率是:
$P(x_i,y_i)=P(y_i=1|x_i)^{y_i}(1-P(y_i=1|x_i))^{1-y_i}=\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}$
解释一下,当$y=1$的时候,后面的那一项没有了,那就只剩下$x$属于1类的概率,当$y=0$的时候,第一项没有了,那就只剩下后面那个$x$属于0的概率。不管$y$是0还是1,上面得到的都是$(x,y)$出现的概率 。那我们的整个样本集,也就是$n$个独立的样本出现的似然函数为(因为每个样本都是独立的,所以$n$的样本出现的概率就是他们各自出现的概率相乘):
似然函数为$\prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}$
对数似然函数为
$L(w)=\sum_{i=1}^N[y_ilog\pi(x_i)+(1-y_i)log(1-\pi(x_i))]$
$=\sum_{i=1}^N \left[ y_ilog{\pi(x_i)\over{1-\pi(x_i)}}+log(1-\pi(x_i)) \right ]$
$=\sum_{i=1}^N[y_i(w\cdot x_i)-log(1+exp(w\cdot x_i))]$
对$L(w)$ 求极大值,得到$w$的估计值。
书上没有写出完整的参数估计算法,但给出了其对数似然函数,经过简单的证明可以得出该函数可以得出该函数是单调上。
我们可以使用$L(w)$作为目标函数,求似然函数的最大值,加个负号,就可以变成最小值,与我们平常的机器学习中的损失函数对应起来。下面对公式进行推导。
$L(w)=\sum_{i=1}^N[y_i(w\cdot x_i)-log(1+exp(w\cdot x_i))]$
$-L(w)=\sum_{i=1}^N[(log(1+exp(w\cdot x_i))-y_i(w\cdot x_i)]$
${\partial (-L(w))\over w}=\sum_{i=1}^N\left({ exp(w\cdot x_i)\cdot x_i \over 1+exp(w\cdot x_i)} - y_i\cdot x_i\right)$
${\partial (-L(w))\over w}=\sum_{i=1}^N\left (\left({ exp(w\cdot x_i) \over 1+exp(w\cdot x_i)} - y_i\right) \cdot x_i\right)$
${\partial (-L(w)) \over w }=\sum_{i=1}^N\left (\left({1 \over 1+exp-(w\cdot x_i)} - y_i\right) \cdot x_i\right)$
我们令导数为0,会发现无法解析求解。没办法,只能借助高大上的迭代来搞定了。这里选用了经典的梯度下降算法。
每次选择一个误分类点,用上述梯度对$w$进行更新即可,注意由于梯度中包含指数操作,所以需要一个很小的学习率。
这样,问题就变成以对数似然函数为目标函数的最优化问题。逻辑斯蒂回归学习中通常采用的方法是梯度下降法及拟牛顿法。
假设$w$的极大似然估计值是$\hat w$ ,那么学到的逻辑斯蒂回归模型为
$P(Y=1|x)={exp(\hat w\cdot x ) \over 1+exp(\hat w \cdot x)}$
$P(Y=0|x)={1 \over 1+exp(\hat w \cdot x)}$
多项逻辑回归
上面介绍的逻辑斯蒂回归模型是二项分类模型,用于二类分类,用于二类分类。可以将其推广为多项逻辑斯蒂回归(multi-nominal logistic regression model),用于多类分类。假设离散型随机变量$Y$的取值集合是${1,2,\dots,K}$,那么多项逻辑回归模型是
$P(Y=k|x)={exp(w_k \cdot x)}\over 1+{\sum_{k=1}^{K-1}exp(w_k\cdot x)}$ ,$k=1,2,\dots,K-1$ ………………..(7)
$P(Y=K|x)={1 \over \sum_{i=1}^{K-1}exp(w_k\cdot x)},k=1,2,\dots,K-1$ ………………..(8)
这里,$x\in R^{n+1},w_k\in R^{n+1}$
二项逻辑斯蒂回归的参数法也可以推广到多项逻辑斯蒂回归。
参考:《统计学习方法》,李航
http://www.hankcs.com/ml/the-logistic-regression-and-the-maximum-entropy-model.html